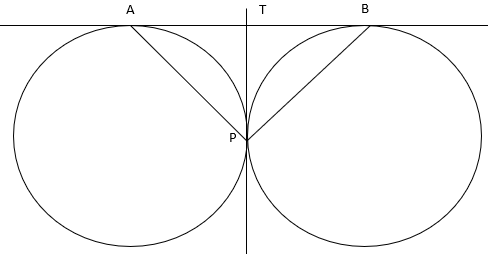
Draw a tangent from a point T on B to P.

Property 1: If two tangents are drawn to a circle from one external point, then their tangent segments (lines joining the external point and the points of tangency on circle) are equal.

Property 2: Sum of all angles of a triangle = 180°.

By property 1,

TA = TP (tangent from T)

TB = TP (tangent from T)

Now in ∆ATP,

TA = TP

∴ ∠APT = ∠PAT

And in ∆BTP,

TB = TP

∴ ∠BPT = ∠PBT

By property 2,

∠APB + ∠PBA + ∠PAB = 180°

⇒ ∠APB + ∠PBT + ∠PAT = 180°

⇒ ∠APB + ∠BPT + ∠ APT = 180° [∵ ∠APT = ∠PAT and ∠BPT = ∠PBT]

⇒ ∠APB + ∠APB = 180° [∵∠APB = ∠BPT + ∠APT]

⇒ 2∠APB = 180°

⇒ ∠APB = 90°

Hence, ∠APB = 90°