Find the equation of a curve passing through origin and satisfying the differential equation 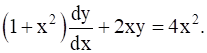
given: ![]() and (0,0) is a solution to the curve
and (0,0) is a solution to the curve
To find: equation of curve satisfying this differential equation
Re-writing the equation as
![]()
Comparing it with ![]()
![]()
![]()
Calculating integrating factor
![]()
![]()
Calculating ![]()
Assume 1+x2=t
2x dx=dt
![]()
Formula: ![]()
Substituting t=1+x2
![]()
![]()
IF=1+x2
Therefore, the solution of the differential equation is given by
![]()
![]()
![]()
Formula: ![]()
Satisfying (0,0) in the curve equation to find c
0=0+c
c=0
therefore, the equation of curve is
![]()
![]()
15