Solve: 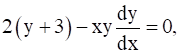 given that y (1) = –2
given that y (1) = –2
given: ![]() and (1, -2) is a solution
and (1, -2) is a solution
To find: solution of given differential equation
Re-writing the equation as
![]()
![]()
![]()
Integrating both sides
![]()
![]()
Formula: ![]()
Substituting (-2,1) to find the value of c
0=-2+c
c=2
⇒ 2 ln x=y-3 ln (y+3) +2
⇒ 2 ln x +3 ln (y+3) =y+2
⇒ 2 ln x +3 ln (y+3) =y+2
⇒ ln x2 + ln (y+3)3 =y+2
⇒ x2(y+3)3 = y + c
20