Solve: 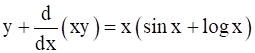
![]()
Now ![]() means differentiation of xy with respect to x
means differentiation of xy with respect to x
Using product rule
![]()
Putting it back in original given differential equation
![]()
![]()
Divide by x
![]()
Compare ![]() with
with ![]()
we get ![]() and Q = sinx + logx
and Q = sinx + logx
This is linear differential equation where P and Q are functions of x
For the solution of linear differential equation, we first need to find the integrating factor
⇒ IF = e∫Pdx
![]()
⇒ IF = e2logx
![]()
⇒ IF = x2
The solution of linear differential equation is given by y(IF) = ∫Q(IF)dx + c
Substituting values for Q and IF
⇒ yx2 = ∫(sinx + logx)x2dx + c
⇒ yx2 = ∫x2sinxdx + ∫x2logxdx + c …(a)
Let us find the integrals ∫x2sinxdx and ∫x2logxdx individually
Using uv rule for integration
⇒ ∫uvdx = u∫vdx - ∫(u’∫v)dx
⇒ ∫x2sinxdx = x2(-cosx) - ∫2x(-cosx)dx
⇒ ∫x2sinxdx = -x2cosx + 2∫xcosxdx
⇒ ∫x2sinxdx = -x2cosx + 2(xsinx - ∫sinxdx)
⇒ ∫x2sinxdx = -x2cosx + 2(xsinx – (-cosx))
⇒ ∫x2sinxdx = -x2cosx + 2xsinx +2cosx …(i)
Now ∫x2logxdx
Again, using product rule



Substitute (i) and (ii) in (a)

Divide by x2
![]()