Solution of 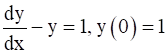 is given by
is given by
![]()
![]()
![]()
Integrate
![]()
⇒ log(1 + y) = x + c …(a)
Now it is given that y(0) = 1 which means when x = 0 y = 1
Hence substitute x = 0 and y = 1 in (a)
⇒ log(1 + y) = x + c
⇒ log(1 + 1) = 0 + c
⇒ c = log2
Put c = log2 back in (a)
⇒ log(1 + y) = x + log2
⇒ log(1 + y) – log2 = x
Using log a – log b = log![]()
![]()
![]()
⇒ 1 + y = 2ex
⇒ y = 2ex – 1
Hence solution of differential equation is y = 2ex – 1
44