The differential equation 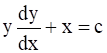 represents:
represents:
![]()
![]()
⇒ y dy = (c – x)dx
Integrate
⇒ y dy = (c – x)dx
⇒ ∫y dy = ∫(c – x)dx
⇒ ∫y dy = ∫c dx – ∫x dx
![]()
k is the integration constant
![]()
![]()
⇒ x2 + y2 = 2cx + k
⇒ x2 + y2 – 2cx – k = 0
This is equation of circle because there is no ‘xy’ term and the coefficient of x2 and y2 is same.
This equation represents family of circles because for different values of c and k we will get different circles
50