(i) xy-plane

Given: Points A(1, -1, 0), B(2, 1, 2) and C(3, 2, -1)

To find: the point on xy-plane which is equidistant from the points

As we know z = 0 in xy-plane.

Let P(x, y, 0) any point in xy-plane

According to the question:

PA = PB = PC

⇒ PA² = PB² = PC²

Formula used:

The distance between any two points (a, b, c) and (m, n, o) is given by,

Therefore,

Distance between P(x, y, 0) and A(1, -1, 0) is PA,

The distance between P(x, y, 0) and B(2, 1, 2) is PB,

Distance between P(x, y, 0) and C(3, 2, -1) is PC,

As PA² = PB²

(x – 1)²+ (y + 1)² = (x – 2)² + (y – 1)² + 4

⇒ x²+ 1 – 2x + y² + 1 + 2y = x²+ 4 – 4x + y² + 1 – 2y + 4

⇒ – 2x + 2 + 2y = 9 – 4x – 2y

⇒ – 2x + 2 + 2y – 9 + 4x + 2y = 0

⇒ 2x + 4y – 7 = 0

⇒ 2x = - 4y + 7……………………(1)

As PA² = PC²

(x – 1)²+ (y + 1)² = (x – 3)² + (y – 2)² + 1

⇒ x²+ 1 – 2x + y² + 1 + 2y = x²+ 9 – 6x + y² + 4 – 4y + 1

⇒ – 2x + 2 + 2y = 14 – 6x – 4y

⇒ – 2x + 2 + 2y – 14 + 6x + 4y = 0

⇒ 4x + 6y – 12 = 0

⇒ 2(2x + 3y – 6) = 0

Put the value of 2x from (1):

⇒ 7 – 4y + 3y – 6 = 0

⇒ – y + 1 = 0

⇒ y = 1

Put this value of y in (1):

2x = 7 – 4y

⇒ 2x = 7 – 4(1)

⇒ 2x = 3

Hence point in xy-plane is equidistant from A, B and C

(ii) yz-plane

Given: Points A(1, -1, 0), B(2, 1, 2) and C(3, 2, -1)

To find: the point on yz-plane which is equidistant from the points

As we know x = 0 in yz-plane.

Let Q(0, y, z) any point in yz-plane

According to the question:

QA = QB = QC

⇒ QA² = QB² = QC²

Formula used:

The distance between any two points (a, b, c) and (m, n, o) is given by,

Therefore,

Distance between Q(0, y, z) and A(1, -1, 0) is QA,

The distance between Q(0, y, Z) and B(2, 1, 2) is QB,

Distance between Q(0, y, z) and C(3, 2, -1) is QC,

As QA² = QB²

1 + z²+ (y + 1)² = (z – 2)² + (y – 1)² + 4

⇒ z²+ 1 + y² + 1 + 2y = z²+ 4 – 4z + y² + 1 – 2y + 4

⇒ 2 + 2y = 9 – 4z – 2y

⇒ 2 + 2y – 9 + 4z + 2y = 0

⇒ 4y + 4z – 7 = 0

⇒ 4z = –4y + 7

As QA² = QC²

1 + z²+ (y + 1)² = (z + 1)² + (y – 2)² + 9

⇒ z²+ 1 + y² + 1 + 2y = z²+ 1 + 2z + y² + 4 – 4y + 9

⇒ 2 + 2y = 14 + 2z – 4y

⇒ 2 + 2y – 14 – 2z + 4y = 0

⇒ –2z + 6y – 12 = 0

⇒ 2(–z + 3y – 6) = 0

Put the value of z from (1):

⇒ 12y + 4y – 7 – 24 = 0

⇒ 16y – 31 = 0

Put this value of y in (1):

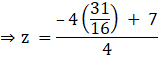
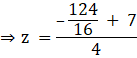
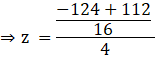
Hence point in yz-plane is equidistant from A, B and C

(iii) xz-plane

Given: Points A(1, -1, 0), B(2, 1, 2) and C(3, 2, -1)

To find: the point on xz-plane which is equidistant from the points

As we know y = 0 in xz-plane.

Let R(x, 0, z) any point in xz-plane

According to the question:

RA = RB = RC

⇒ RA² = RB² = RC²

Formula used:

The distance between any two points (a, b, c) and (m, n, o) is given by,

Therefore,

Distance between R(x, 0, z) and A(1, -1, 0) is RA,

Distance between R(x, 0, z) and B(2, 1, 2) is RB,

Distance between R(x, 0, z) and C(3, 2, -1) is RC,

As RA² = RB²

1 + z²+ (x – 1)² = (z – 2)² + (x – 2)² + 1

⇒ z²+ 1 + x² + 1 – 2x = z²+ 4 – 4z + x² + 4 – 4x + 1

⇒ 2 – 2x = 9 – 4z – 4x

⇒ 2 + 4z – 9 + 4x – 2x = 0

⇒ 2x + 4z – 7 = 0

⇒ 2x = –4z + 7……………………………(1)

As RA² = RC²

1 + z²+ (x – 1)² = (z + 1)² + (x – 3)² + 4

⇒ z²+ 1 + x² + 1 – 2x = z²+ 1 + 2z + x² + 9 – 6x + 4

⇒ 2 – 2x = 14 + 2z – 6x

⇒ 2 – 2x – 14 – 2z + 6x = 0

⇒ –2z + 4x – 12 = 0

⇒ 2(2x) = 12 + 2z

Put the value of 2x from (1):

⇒ 2(–4z + 7) = 12 + 2z

⇒ –8z + 14 = 12 + 2z

⇒ 14 – 12 = 8z + 2z

⇒ 10z = 2

Put this value of z in (1):

Hence point in xz-plane is equidistant from A, B and C