Given: point P(3, 4, 5)

To find: distance of the point P from the z-axis

Formula used:

The distance between any two points (a, b, c) and (m, n, o) is given by,

As, x and y coordinate on z-axis are zero

Let point D on z-axis is (0, 0, z)

Direction cosines of z-axis are (0, 0, 1)

Direction cosines of PD are (3 – 0, 4 – 0, 5 – z) = (3, 4, 5 – z)

Let are two vectors as shown in the figure:

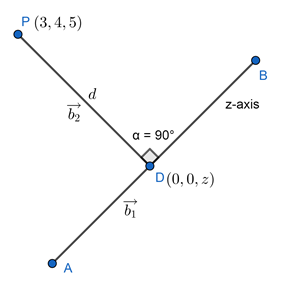
The dot product of perpendicular vectors is always zero

Therefore,

⇒ 3 × 0 + 4 × 0 + (5 – z) × 1 = 0

⇒ 0 + 0 + 5 – z = 0

⇒ z = 5

Hence point D(0, 0, 5)

Distance between point P(3, 4, 5) and D(0, 0, 5) is d

= 5

Hence, the distance of the point P from z-axis is 5 units