Show that the set of all points such that the difference of their distances from (4, 0) and (-4, 0) is always equal to 2 represents a hyperbola.
To prove: the set of all points under given conditions represents a hyperbola
Let a point P be (x, y) such that the difference of their distances from (4, 0) and (-4, 0) is always equal to 2.
Formula used:
The distance between two points (m, n) and (a, b) is given by
![]()
The distance of P(x, y) from (4, 0) is ![]()
The distance of P(x, y) from (-4, 0) is ![]()
Since, the difference of their distances from (4, 0) and (-4, 0) is always equal to 2
Therefore,
![]()
![]()
Squaring both sides:
![]()
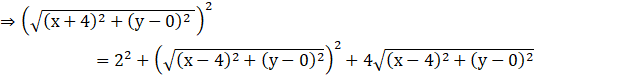
![]()
![]()
![]()
![]()
![]()
![]()
Squaring both sides:
![]()
⇒ 16x2 + 1 – 8x = (x – 4)2 + y2
⇒ 16x2 + 1 – 8x = x2 + 16 – 8x + y2
⇒ 16x2 + 1 – 8x – x2 – 16 + 8x – y2 = 0
⇒ 15x2 – y2 – 15 = 0
Hence, required equation of hyperbola is 15x2 – y2 – 15 = 0