Given: Foci are (6, 4) and (-4, 4) and eccentricity is 2

To find: equation of the hyperbola

Formula used:

Standard form of the equation of hyperbola is,

Center is the mid-point of two foci.

Distance between the foci is 2ae and b² = a²(e² – 1)

Distance between two points (m, n) and (a, b) is given by

Mid-point theorem:

Mid-point of two points (m, n) and (a, b) is given by

Center of hyperbola having foci (6, 4) and (-4, 4) is given by

= (1, 4)

Distance between the foci is 2ae and Foci are (6, 4) and (-4, 4)

{∵ e = 2}

b² = a²(e² – 1)

Equation of hyperbola:

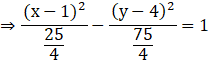
Hence, required equation of hyperbola is