The key point to solve the problem:

The idea of cosine formula in ΔABC

Cos A = 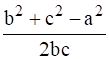Cos B = 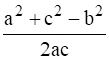Cos C = .

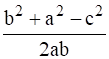As we have to prove : (a + b + c) (a – b + c) = 3ca

LHS = (a + c+ b) (a + c– b) = (a + c)² – b² { using ( x + y )( x – y ) = x² – y² }

Now the above expression gives us hint that we need to apply cosine formula as terms has resemblance.

∴ cos B =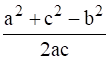

cos 60° =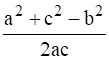

⇒ =

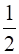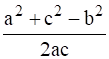
∴ ac =

Adding 2bc both sides to get the term present in final term-

∴ 3ac = a² + c² + 2ac – b²

⇒ 3ac = (a + c)² – b²

using ( x + y )( x – y ) = x² – y² , we have –

3ac = (a + c+ b) (a + c– b)

Or (a + b + c) (a – b + c) = 3ca …Hence proved