Ideas required to solve the problem:

The general solution of any trigonometric equation is given as –

• sin x = sin y, implies x = nπ + (– 1)ⁿy, where n ∈ Z.

• cos x = cos y, implies x = 2nπ ± y, where n ∈ Z.

• tan x = tan y, implies x = nπ + y, where n ∈ Z.

given,

.

In all such problems we try to reduce the equation in an equation involving single trigonometric expression.

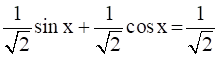∴ { dividing by √2 both sides}

⇒ { ∵ }

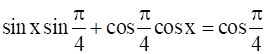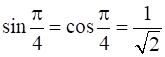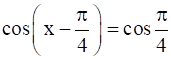⇒ { ∵ cos A cos B + sin A sin B = cos (A - B)}

NOTE: We can also make the ratio of sin instead of cos , the answer remains same but the form of answer may look different, when you put values of n you will get same values with both forms

If cos x = cos y, implies x = 2nπ ± y, where n ∈ Z

∴ s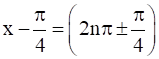

∴ .

.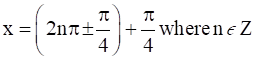
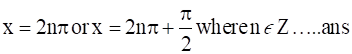