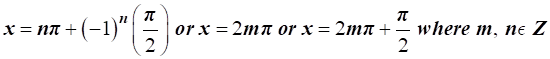Ideas required to solve the problem:

The general solution of any trigonometric equation is given as –

• sin x = sin y, implies x = nπ + (– 1)ⁿy, where n ∈ Z.

• cos x = cos y, implies x = 2nπ ± y, where n ∈ Z.

• tan x = tan y, implies x = nπ + y, where n ∈ Z.

Given,

3 – 2 cos x – 4 sin x – cos 2x + sin 2x = 0

As, cos 2x = 1 – 2sin² x and sin 2x = 2sin x cos x

∴ 3 – 2cos x – 4sin x – (1 – 2sin² x) + 2sin x cos x = 0

⇒ 2sin² x – 4sin x + 2 – 2cos x + 2sin x cos x = 0

⇒ 2(sin² x – 2sin x + 1) + 2cos x(sin x – 1) = 0

⇒ 2(sin x – 1)² + 2cos x(sin x – 1) = 0

⇒ (sin x – 1)(2cos x + 2sin x – 2) = 0

∴ sin x = 1 or sin x + cos x = 1

When, sin x = 1

We have,

sin x = sin π/2

If sin x = sin y, implies x = nπ + (– 1)ⁿy, where n ∈ Z

∴

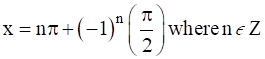
When, sin x + cos x = 1

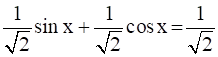∴ { dividing by √2 both sides}

⇒ { ∵ }

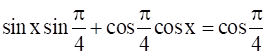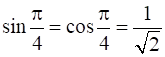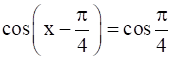⇒ { ∵ cos A cos B + sin A sin B = cos (A - B)}

If cos x = cos y, implies x = 2mπ ± y, where m ∈ Z

∴

∴

⇒

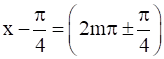
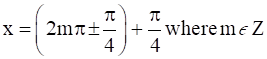
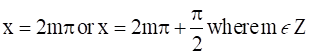
Hence,