Find the modulus and argument of the following complex numbers and hence express each of them in the polar form :

Question

Philoid · Accepted Answer

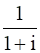
Given complex number is .

⇒

We know that i²=-1

⇒

We know that the polar form of a complex number Z=x+iy is given by Z=|Z|(cosθ+isinθ)

Where,

|Z|=modulus of complex number=

θ =arg(z)=argument of complex number=

Now for the given problem,

⇒

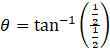
Since x>0,y<0 complex number lies in 4^th quadrant and the value of θ will be as follows -90⁰≤θ≤0⁰.

⇒

⇒ .

⇒

∴ The Polar form of is .