Given Complex number is z=1-sin+icos

We know that sin²θ+cos²θ=1, sin2θ=2sinθcosθ, cos2θ=cos²θ-sin²θ.

⇒

⇒

e know that the polar form of a complex number Z=x+iy is given by Z=|Z|(cosθ+isinθ)

Where,

|Z|=modulus of complex number=

θ =arg(z)=argument of complex number=

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

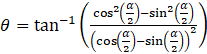
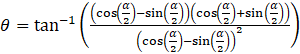
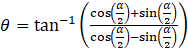
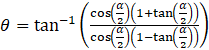
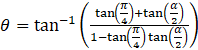
We know that sine and cosine functions are periodic with period 2

Here We have 3 intervals as follows:

(i)

(ii)

(iii)

Case(i):

In the interval , and also

so,

⇒

⇒

⇒

⇒ .(∵ θ lies in 1^st quadrant)

∴ The polar form is .

Case(ii):

In the interval , and also

so,

⇒

⇒

⇒

⇒

⇒ . (∵ θ lies in 4^th quadrant)

⇒

∴ The polar form is .

Case(iii):

In the interval , and also

so,

⇒

⇒

⇒

⇒

⇒ .(since θ presents in first quadrant and tan’s period is )

⇒ .

∴ The polar form is .