Table of Contents
Chapter Three
Motion in a Straight Line
3.1 Introduction
Motion is common to everything in the universe. We walk, run and ride a bicycle. Even when we are sleeping, air moves into and out of our lungs and blood flows in arteries and veins. We see leaves falling from trees and water flowing down a dam. Automobiles and planes carry people from one place to the other. The earth rotates once every twenty-four hours and revolves round the sun once in a year. The sun itself is in motion in the Milky Way, which is again moving within its local group of galaxies.
Motion is change in position of an object with time. How does the position change with time ? In this chapter, we shall learn how to describe motion. For this, we develop the concepts of velocity and acceleration. We shall confine ourselves to the study of motion of objects along a straight line, also known as rectilinear motion. For the case of rectilinear motion with uniform acceleration, a set of simple equations can be obtained. Finally, to understand the relative nature of motion, we introduce the concept of relative velocity.
In our discussions, we shall treat the objects in motion as point objects. This approximation is valid so far as the size of the object is much smaller than the distance it moves in a reasonable duration of time. In a good number of situations in real-life, the size of objects can be neglected and they can be considered as point-like objects without much error.
In Kinematics, we study ways to describe motion without going into the causes of motion. What causes motion described in this chapter and the next chapter forms the subject matter of Chapter 5.
3.2 Position, path length and displacement
Earlier you learnt that motion is change in position of an object with time. In order to specify position, we need to use a reference point and a set of axes. It is convenient to choose a rectangular coordinate system consisting of three mutually perpenducular axes, labelled X-, Y-, and Z- axes. The point of intersection of these three axes is called origin (O) and serves as the reference point. The coordinates (x, y. z) of an object describe the position of the object with respect to this coordinate system. To measure time, we position a clock in this system. This coordinate system along with a clock constitutes a frame of reference.
If one or more coordinates of an object change with time, we say that the object is in motion. Otherwise, the object is said to be at rest with respect to this frame of reference.
The choice of a set of axes in a frame of reference depends upon the situation. For example, for describing motion in one dimension, we need only one axis. To describe motion in two/three dimensions, we need a set of two/three axes.
Description of an event depends on the frame of reference chosen for the description. For example, when you say that a car is moving on a road, you are describing the car with respect to a frame of reference attached to you or to the ground. But with respect to a frame of reference attached with a person sitting in the car, the car is at rest.
To describe motion along a straight line, we can choose an axis, say X-axis, so that it coincides with the path of the object. We then measure the position of the object with reference to a conveniently chosen origin, say O, as shown in Fig. 3.1. Positions to the right of O are taken as positive and to the left of O, as negative. Following this convention, the position coordinates of point P and Q in Fig. 3.1 are +360 m and +240 m. Similarly, the position coordinate of point R is –120 m.
Path length
Consider the motion of a car along a straight line. We choose the x-axis such that it coincides with the path of the car’s motion and origin of the axis as the point from where the car started moving, i.e. the car was at x = 0 at t = 0 (Fig.3.1). Let P, Q and R represent the positions of the car at different instants of time. Consider two cases of motion. In the first case, the car moves from O to P. Then the distance moved by the car is OP = +360 m. This distance is called the path length traversed by the car. In the second case, the car moves from O to P and then moves back from P to Q. During this course of motion, the path length traversed is OP + PQ = + 360 m + (+120 m) = + 480 m. Path length is a scalar quantity — a quantity that has a magnitude only and no direction (see Chapter 4).
Displacement
It is useful to define another quantity displacement as the change in position. Let x1 and x2 be the positions of an object at time t1 and t2. Then its displacement, denoted by ∆x, in time ∆t = (t2 - t1), is given by the difference between the final and initial positions :
∆x = x2 – x1
(We use the Greek letter delta (∆) to denote a change in a quantity.)
If x2 > x1, ∆x is positive; and if x2 < x1, ∆x is negative.
Displacement has both magnitude and direction. Such quantities are represented by vectors. You will read about vectors in the next chapter. Presently, we are dealing with motion along a straight line (also called rectilinear motion) only. In one-dimensional motion, there are only two directions (backward and forward, upward and downward) in which an object can move, and these two directions can easily be specified by + and – signs. For example, displacement of the car in moving from O to P is :
∆x = x2 – x1 = (+360 m) – 0 m = +360 m
The displacement has a magnitude of 360 m and is directed in the positive x direction as indicated by the + sign. Similarly, the displacement of the car from P to Q is 240 m – 360 m = – 120 m. The negative sign indicates the direction of displacement. Thus, it is not necessary to use vector notation for discussing motion of objects in one-dimension.
The magnitude of displacement may or may not be equal to the path length traversed by an object. For example, for motion of the car from O to P, the path length is +360 m and the displacement is +360 m. In this case, the magnitude of displacement (360 m) is equal to the path length (360 m). But consider the motion of the car from O to P and back to Q. In this case, the path length = (+360 m) + (+120 m) = + 480 m. However, the displacement = (+240 m) – (0 m) = + 240 m. Thus, the magnitude of displacement (240 m) is not equal to the path length (480 m).

The magnitude of the displacement for a course of motion may be zero but the corresponding path length is not zero. For example, if the car starts from O, goes to P and then returns to O, the final position coincides with the initial position and the displacement is zero. However, the path length of this journey is OP + PO = 360 m + 360 m = 720 m.
Motion of an object can be represented by a position-time graph as you have already learnt about it. Such a graph is a powerful tool to represent and analyse different aspects of motion of an object. For motion along a straight line, say X-axis, only x-coordinate varies with time and we have an x-t graph. Let us first consider the simple case in which an object is stationary, e.g. a car standing still at x = 40 m. The position-time graph is a straight line parallel to the time axis, as shown in Fig. 3.2(a).
If an object moving along the straight line covers equal distances in equal intervals of time, it is said to be in uniform motion along a straight line. Fig. 3.2(b) shows the position-time graph of such a motion.
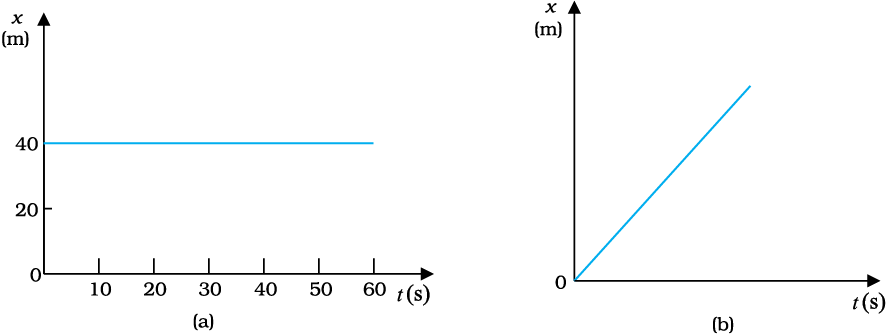
Fig. 3.2 Position-time graph of (a) stationary object, and (b) an object in uniform motion.
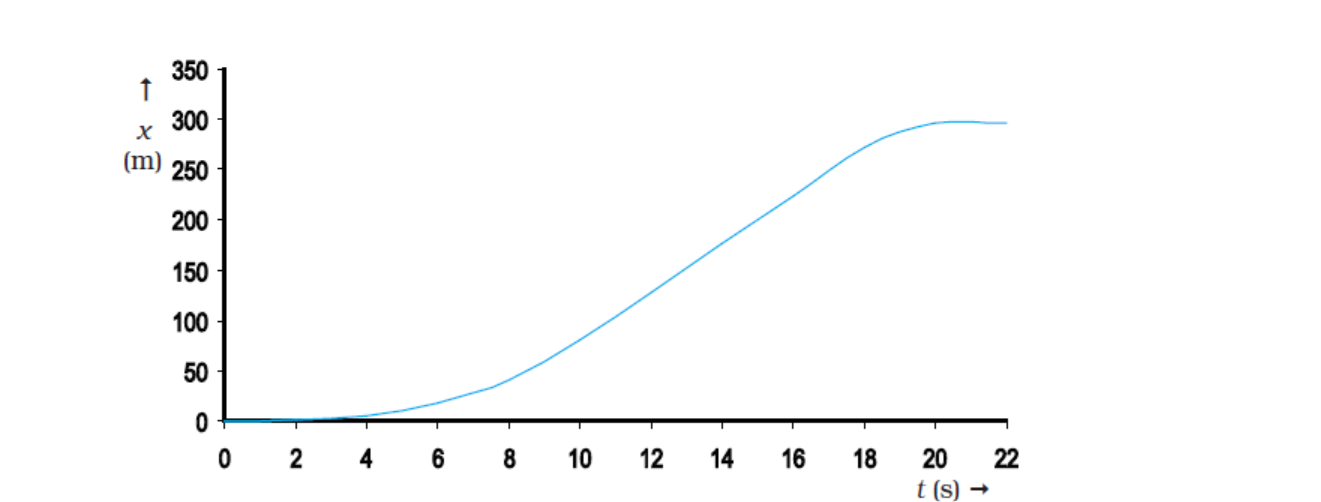
Fig. 3.3 Position-time graph of a car.
Now, let us consider the motion of a car that starts from rest at time t = 0 s from the origin O and picks up speed till t = 10 s and thereafter moves with uniform speed till t = 18 s. Then the brakes are applied and the car stops at
t = 20 s and x = 296 m. The position-time graph for this case is shown in Fig. 3.3. We shall refer to this graph in our discussion in the following sections.
3.3 Average velocity and average speed
When an object is in motion, its position changes with time. But how fast is the position changing with time and in what direction? To describe this, we define the quantity average velocity. Average velocity is defined as the change in position or displacement (∆x) divided by the time intervals (∆t), in which the displacement occurs :
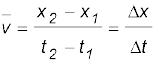 (3.1)
(3.1)
where x2 and x1 are the positions of the object at time t2and t1, respectively. Here the bar over the symbol for velocity is a standard notation used to indicate an average quantity. The SI unit for velocity is m/s or m s–1, although km h–1 is used in many everyday applications.
Like displacement, average velocity is also a vector quantity. But as explained earlier, for motion in a straight line, the directional aspect of the vector can be taken care of by + and – signs and we do not have to use the vector notation for velocity in this chapter.
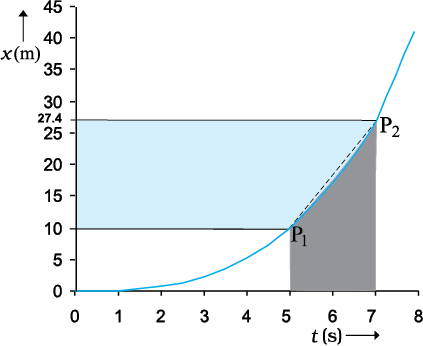
Fig. 3.4 The average velocity is the slope of line P1P2.
Consider the motion of the car in Fig. 3.3. The portion of the x-t graph between t = 0 s and t = 8 s is blown up and shown in Fig. 3.4. As seen from the plot, the average velocity of the car between time t = 5 s and t = 7 s is :
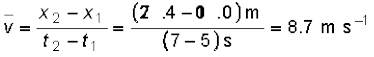
Geometrically, this is the slope of the straight line P1P2 connecting the initial position  to the final position P2 as shown in Fig. 3.4.
to the final position P2 as shown in Fig. 3.4.
The average velocity can be positive or negative depending upon the sign of the displacement. It is zero if the displacement is zero. Fig. 3.5 shows the x-t graphs for an object, moving with positive velocity (Fig. 3.5a), moving with negative velocity (Fig. 3.5b) and at rest (Fig. 3.5c).

Fig. 3.5 Position-time graph for an object (a) moving with positive velocity, (b) moving with negative velocity, and (c) at rest.
Average velocity as defined above involves only the displacement of the object. We have seen earlier that the magnitude of displacement may be different from the actual path length. To describe the rate of motion over the actual path, we introduce another quantity called average speed.
Average speed is defined as the total path length travelled divided by the total time interval during which the motion has taken place :
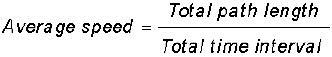 (3.2)
(3.2)
Average speed has obviously the same unit (m s–1) as that of velocity. But it does not tell us in what direction an object is moving. Thus, it is always positive (in contrast to the average velocity which can be positive or negative). If the motion of an object is along a straight line and in the same direction, the magnitude of displacement is equal to the total path length. In that case, the magnitude of average velocity is equal to the average speed. This is not always the case, as you will see in the following example.
Example 3.1 A car is moving along a straight line, say OP in Fig. 3.1. It moves from O to P in 18 s and returns from P to Q in 6.0 s. What are the average velocity and average speed of the car in going (a) from O to P ? and (b) from O to P and back to Q ?
Answer (a)
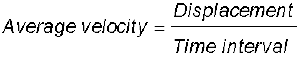
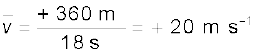
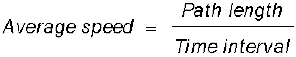
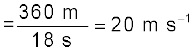
Thus, in this case the average speed is equal to the magnitude of the average velocity.
(b) In this case,
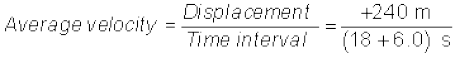
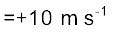
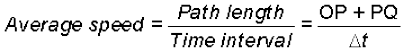
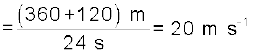
Thus, in this case the average speed is not equal to the magnitude of the average velocity. This happens because the motion here involves change in direction so that the path length is greater than the magnitude of displacement. This shows that speed is, in general, greater than the magnitude of the velocity. If the car in Example 3.1 moves from O to P and comes back to O in the same time interval, average speed is 20 m/s but the average velocity is zero !
3.4 Instantaneous velocity and speed
The average velocity tells us how fast an object has been moving over a given time interval but does not tell us how fast it moves at different instants of time during that interval. For this, we define instantaneous velocity or simply velocity v at an instant t.
The velocity at an instant is defined as the limit of the average velocity as the time interval ∆t becomes infinitesimally small. In other words,
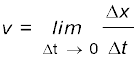 (3.3a)
(3.3a)
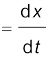 (3.3b)
(3.3b)
where the symbol 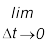 stands for the operation of taking limit as ∆t0 of the quantity on its right. In the language of calculus, the quantity on the right hand side of Eq. (3.3a) is the differential coefficient of x with respect to t and is denoted by
stands for the operation of taking limit as ∆t0 of the quantity on its right. In the language of calculus, the quantity on the right hand side of Eq. (3.3a) is the differential coefficient of x with respect to t and is denoted by 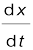 (see Appendix 3.1). It is the rate of change of position with respect to time, at that instant.
(see Appendix 3.1). It is the rate of change of position with respect to time, at that instant.
We can use Eq. (3.3a) for obtaining the value of velocity at an instant either graphically or numerically. Suppose that we want to obtain graphically the value of velocity at time
t = 4 s (point P) for the motion of the car represented in Fig. 3.3. The figure has been redrawn in Fig.3.6 choosing different scales to facilitate the calculation.
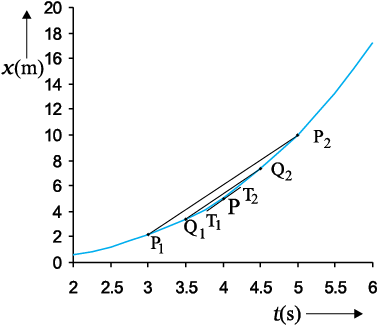
Fig. 3.6 Determining velocity from position-time graph. Velocity at t = 4 s is the slope of the tangent to the graph at that instant.
Let us take ∆t = 2 s centred at t = 4 s. Then, by the definition of the average velocity, the slope of line P1P2 ( Fig. 3.6) gives the value of average velocity over the interval 3 s to 5 s. Now, we decrease the value of ∆t from 2 s to 1 s. Then line P1P2 becomes Q1Q2 and its slope gives the value of the average velocity over the interval 3.5 s to 4.5 s. In the limit ∆t → 0, the line P1P2 becomes tangent to the position-time curve at the point P and the velocity at t = 4 s is given by the slope of the tangent at that point. It is difficult to show this process graphically. But if we use numerical method to obtain the value of the velocity, the meaning of the limiting process becomes clear. For the graph shown in
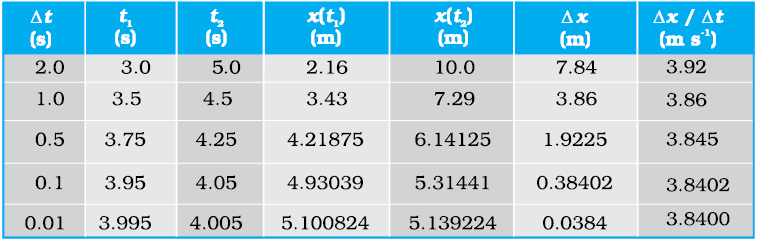
Fig. 3.6, x = 0.08 t3. Table 3.1 gives the value of ∆x/∆t calculated for ∆t equal to 2.0 s, 1.0 s, 0.5 s, 0.1 s and 0.01 s centred at t = 4.0 s. The second and third columns give the value of t1= 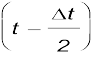 and
and 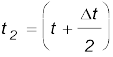 and the fourth and the fifth columns give the corresponding values of x, i.e. x (t1) = 0.08
and the fourth and the fifth columns give the corresponding values of x, i.e. x (t1) = 0.08 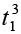 and x (t2) = 0.08
and x (t2) = 0.08 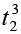 . The sixth column lists the difference ∆x = x (t2) – x (t1) and the last column gives the ratio of ∆x and ∆t, i.e. the average velocity corresponding to the value of ∆t listed in the first column.
. The sixth column lists the difference ∆x = x (t2) – x (t1) and the last column gives the ratio of ∆x and ∆t, i.e. the average velocity corresponding to the value of ∆t listed in the first column.
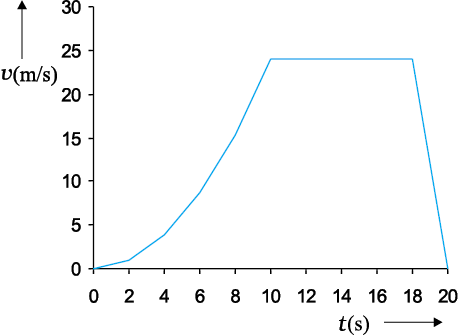
We see from Table 3.1 that as we decrease the value of ∆t from 2.0 s to 0.010 s, the value of the average velocity approaches the limiting value 3.84 m s–1 which is the value of velocity at t = 4.0 s, i.e. the value of 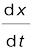 at t = 4.0 s. In this manner, we can calculate velocity at each instant for motion of the car shown in Fig. 3.3. For this case, the variation of velocity with time is found to be as shown in Fig. 3.7.
at t = 4.0 s. In this manner, we can calculate velocity at each instant for motion of the car shown in Fig. 3.3. For this case, the variation of velocity with time is found to be as shown in Fig. 3.7.
The graphical method for the determination of the instantaneous velocity is always not a convenient method. For this, we must carefully plot the position–time graph and calculate the value of average velocity as ∆t becomes smaller and smaller. It is easier to calculate the value of velocity at different instants if we have data of positions at different instants or exact expression for the position as a function of time. Then, we calculate ∆x/∆t from the data for decreasing the value of ∆t and find the limiting value as we have done in Table 3.1 or use differential calculus for the given expression and calculate 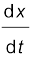 at different instants as done in the following example.
at different instants as done in the following example.
Table 3.1 Limiting value of 2809.png at t = 4 s
Example 3.2 The position of an object moving along x-axis is given by x = a + bt2 where a = 8.5 m, b = 2.5 m s–2 and t is measured in seconds. What is its velocity at t = 0 s and t = 2.0 s. What is the average velocity between t = 2.0 s and t = 4.0 s ?
Answer In notation of differential calculus, the velocity is
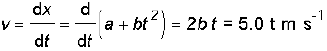
At t = 0 s, v = 0 m s–1 and at t = 2.0 s, v = 10 m s-1 .
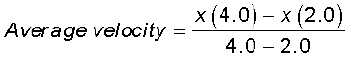
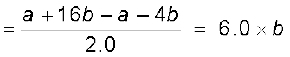
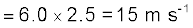
From Fig. 3.7, we note that during the period t =10 s to 18 s the velocity is constant. Between period t =18 s to t = 20 s, it is uniformly decreasing and during the period t = 0 s to t = 10 s, it is increasing. Note that for uniform motion, velocity is the same as the average velocity at all instants.
Instantaneous speed or simply speed is the magnitude of velocity. For example, a velocity of + 24.0 m s–1 and a velocity of – 24.0 m s–1 — both have an associated speed of 24.0 m s-1. It should be noted that though average speed over a finite interval of time is greater or equal to the magnitude of the average velocity, instantaneous speed at an instant is equal to the magnitude of the instantaneous velocity at that instant. Why so?
3.5 Acceleration
The velocity of an object, in general, changes during its course of motion. How to describe this change? Should it be described as the rate of change in velocity with distance or with time ? This was a problem even in Galileo’s time. It was first thought that this change could be described by the rate of change of velocity with distance. But, through his studies of motion of freely falling objects and motion of objects on an inclined plane, Galileo concluded that the rate of change of velocity with time is a constant of motion for all objects in free fall. On the other hand, the change in velocity with distance is not constant – it decreases with the increasing distance of fall. This led to the concept of acceleration as the rate of change of velocity with time.
The average acceleration  over a time interval is defined as the change of velocity divided by the time interval :
over a time interval is defined as the change of velocity divided by the time interval :
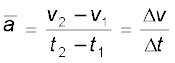 (3.4)
(3.4)
where v2 and v1 are the instantaneous velocities or simply velocities at time t2 and t1 . It is the average change of velocity per unit time. The SI unit of acceleration is m s–2 .
On a plot of velocity versus time, the average acceleration is the slope of the straight line connecting the points corresponding to (v2, t2) and (v1, t1). The average acceleration
for velocity-time graph shown in Fig. 3.7 for different time intervals 0 s - 10 s, 10 s – 18 s, and 18 s – 20 s are :
0 s - 10 s 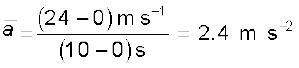
10 s - 18 s 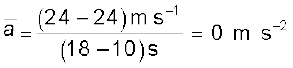
18 s - 20 s 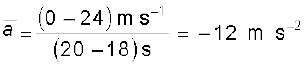
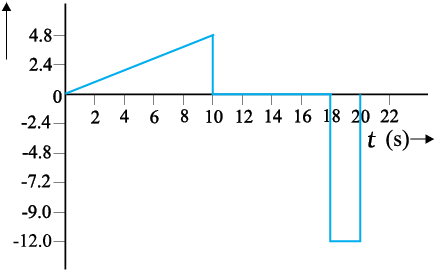
Fig. 3.8 Acceleration as a function of time for motion represented in Fig. 3.3.
Instantaneous acceleration is defined in the same way as the instantaneous velocity :
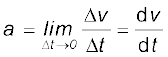 (3.5)
(3.5)
The acceleration at an instant is the slope of the tangent to the v–t curve at that instant. For the v–t curve shown in Fig. 3.7, we can obtain acceleration at every instant of time. The resulting a – t curve is shown in Fig. 3.8. We see that the acceleration is nonuniform over the period 0 s to 10 s. It is zero between 10 s and
18 s and is constant with value –12 m s–2 between 18 s and 20 s. When the acceleration is uniform, obviously, it equals the average acceleration over that period.
Since velocity is a quantity having both magnitude and direction, a change in velocity may involve either or both of these factors. Acceleration, therefore, may result from a change in speed (magnitude), a change in direction or changes in both. Like velocity, acceleration can also be positive, negative or zero. Position-time graphs for motion with positive, negative and zero acceleration are shown in Figs. 3.9 (a), (b) and (c), respectively. Note that the graph curves upward for positive acceleration; downward for negative acceleration and it is a straight line for zero acceleration. As an exercise, identify in Fig. 3.3, the regions of the curve that correspond to these three cases.
Although acceleration can vary with time, our study in this chapter will be restricted to motion with constant acceleration. In this case, the average acceleration equals the constant value of acceleration during the interval. If the velocity of an object is vo at t = 0 and v at time t, we have
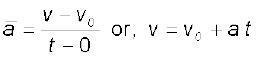 (3.6)
(3.6)

Fig. 3.9 Position-time graph for motion with (a) positive acceleration; (b) negative acceleration, and (c) zero acceleration.
Let us see how velocity-time graph looks like for some simple cases. Fig. 3.10 shows velocity-time graph for motion with constant acceleration for the following cases :
(a) An object is moving in a positive direction with a positive acceleration, for example the motion of the car in Fig. 3.3 between t = 0 s and t = 10 s.
(b) An object is moving in positive direction with a negative acceleration, for example, motion of the car in Fig 3.3 between
t = 18 s and 20 s.
(c) An object is moving in negative direction with a negative acceleration, for example the motion of a car moving from O in Fig. 3.1 in negative x-direction with increasing speed.
(d) An object is moving in positive direction till time t1, and then turns back with the same negative acceleration, for example the motion of a car from point O to point Q in Fig. 3.1 till time t1 with decreasing speed and turning back and moving with the same negative acceleration.
An interesting feature of a velocity-time graph for any moving object is that the area under the curve represents the displacement over a given time interval. A general proof of this statement requires use of calculus.
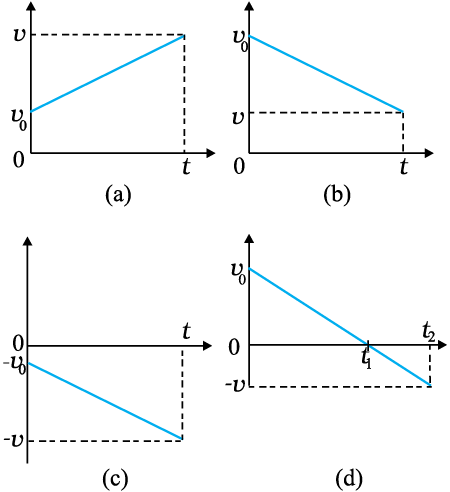
Fig. 3.10 Velocity–time graph for motions with constant acceleration. (a) Motion in positive direction with positive acceleration, (b) Motion in positive direction with negative acceleration, (c) Motion in negative direction with negative acceleration, (d) Motion of an object with negative acceleration that changes direction at time t1. Between times 0 to t1, its moves in positive x - direction and between t1 and t2 it moves in the opposite direction.
We can, however, see that it is true for the simple case of an object moving with constant velocity u. Its velocity-time graph is as shown in Fig. 3.11.

Fig. 3.11 Area under v–t curve equals displacement of the object over a given tim
interval.
The v-t curve is a straight line parallel to the time axis and the area under it between t = 0 and t = T is the area of the rectangle of height u and base T. Therefore, area = u × T = uT which is the displacement in this time interval. How come in this case an area is equal to a distance? Think! Note the dimensions of quantities on the two coordinate axes, and you will arrive at the answer.
Note that the x-t, v-t, and a-t graphs shown in several figures in this chapter have sharp kinks at some points implying that the functions are not differentiable at these points. In any realistic situation, the functions will be differentiable at all points and the graphs will be smooth.
What this means physically is that acceleration and velocity cannot change values abruptly at an instant. Changes are always continuous.
3.6 Kinematic equations for uniformly accelerated motion
For uniformly accelerated motion, we can derive some simple equations that relate displacement (x), time taken (t), initial velocity (v0), final velocity (v) and acceleration (a). Equation (3.6) already obtained gives a relation between final and initial velocities v and v0 of an object moving with uniform acceleration a :
v = v0 + at (3.6)
This relation is graphically represented in Fig. 3.12.
The area under this curve is :
Area between instants 0 and t = Area of triangle ABC + Area of rectangle OACD
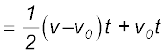
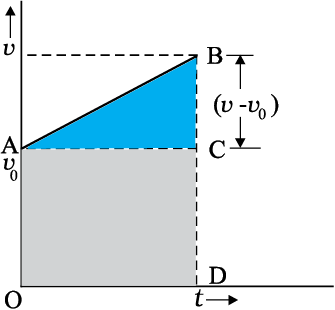
Fig. 3.12 Area under v-t curve for an object with uniform acceleration.
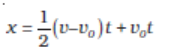 (3.7)
(3.7)
But 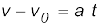
Therefore, 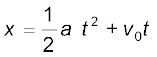
or, 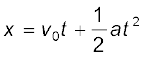 (3.8)
(3.8)
Equation (3.7) can also be written as
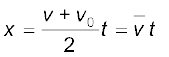 (3.9a)
(3.9a)
where,
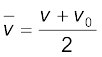 (constant acceleration only) (3.9b)
(constant acceleration only) (3.9b)
Equations (3.9a) and (3.9b) mean that the object has undergone displacement x with an average velocity equal to the arithmetic average of the initial and final velocities.
From Eq. (3.6), t = (v – v0)/a. Substituting this in Eq. (3.9a), we get
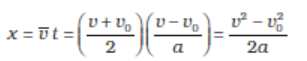
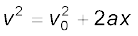 (3.10)
(3.10)
This equation can also be obtained by substituting the value of t from Eq. (3.6) into Eq. (3.8). Thus, we have obtained three important equations :
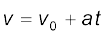
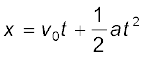
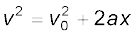 (3.11a)
(3.11a)
connecting five quantities v0, v, a, t and x. These are kinematic equations of rectilinear motion for constant acceleration.
The set of Eq. (3.11a) were obtained by assuming that at t = 0, the position of the particle, x is 0. We can obtain a more general equation if we take the position coordinate at t = 0 as non-zero, say x0. Then Eqs. (3.11a) are modified (replacing x by x – x0 ) to :
