Chapter Twelve

Thermodynamics

12.1 INTRODUCTION  

In previous chapter we have studied thermal properties of matter. In this chapter we shall study laws that govern thermal energy. We shall study the processes where work is converted into heat and vice versa. In winter, when we rub our palms together, we feel warmer; here work done in rubbing produces the ‘heat’. Conversely, in a steam engine, the ‘heat’ of the steam is used to do useful work in moving the pistons, which in turn rotate the wheels of the train.

In physics, we need to define the notions of heat, temperature, work, etc. more carefully. Historically, it took a long time to arrive at the proper concept of ‘heat’. Before the modern picture, heat was regarded as a fine invisible fluid filling in the pores of a substance. On contact between a hot body and a cold body, the fluid (called caloric) flowed from the colder to the hotter body! This is similar to what happens when a horizontal pipe connects two tanks containing water up to different heights. The flow continues until the levels of water in the two tanks are the same. Likewise, in the ‘caloric’ picture of heat, heat flows until the ‘caloric levels’ (i.e., the temperatures) equalise.

In time, the picture of heat as a fluid was discarded in favour of the modern concept of heat as a form of energy. An important experiment in this connection was due to Benjamin Thomson (also known as Count Rumford) in 1798. He observed that boring of a brass cannon generated a lot of heat, indeed enough to boil water. More significantly, the amount of heat produced depended on the work done (by the horses employed for turning the drill) but not on the sharpness of the drill. In the caloric picture, a sharper drill would scoop out more heat fluid from the pores; but this was not observed. A most natural explanation of the observations was that heat was a form of energy and the experiment demonstrated conversion of energy from one form to another–from work to heat.

Thermodynamics is the branch of physics that deals with the concepts of heat and temperature and the inter-conversion of heat and other forms of energy. Thermodynamics is a macroscopic science. It deals with bulk systems and does not go into the molecular constitution of matter. In fact, its concepts and laws were formulated in the nineteenth century before the molecular picture of matter was firmly established. Thermodynamic description involves relatively few macroscopic variables of the system, which are suggested by common sense and can be usually measured directly. A microscopic description of a gas, for example, would involve specifying the co-ordinates and velocities of the huge number of molecules constituting the gas. The description in kinetic theory of gases is not so detailed but it does involve molecular distribution of velocities. Thermodynamic description of a gas, on the other hand, avoids the molecular description altogether. Instead, the state of a gas in thermodynamics is specified by macroscopic variables such as pressure, volume, temperature, mass and composition that are felt by our sense perceptions and are measurable*.

The distinction between mechanics and thermodynamics is worth bearing in mind. In mechanics, our interest is in the motion of particles or bodies under the action of forces and torques. Thermodynamics is not concerned with the motion of the system as a whole. It is concerned with the internal macroscopic state of the body. When a bullet is fired from a gun, what changes is the mechanical state of the bullet (its kinetic energy, in particular), not its temperature. When the bullet pierces a wood and stops, the kinetic energy of the bullet gets converted into heat, changing the temperature of the bullet and the surrounding layers of wood. Temperature is related to the energy of the internal (disordered) motion of the bullet, not to the motion of the bullet as a whole.

12.2 Thermal equilibrium

Equilibrium in mechanics means that the net external force and torque on a system are zero. The term ‘equilibrium’ in thermodynamics appears in a different context : we say the state of a system is an equilibrium state if the macroscopic variables that characterise the system do not change in time. For example, a gas inside a closed rigid container, completely insulated from its surroundings, with fixed values of pressure, volume, temperature, mass and composition that do not change with time, is in a state of thermodynamic equilibrium. 

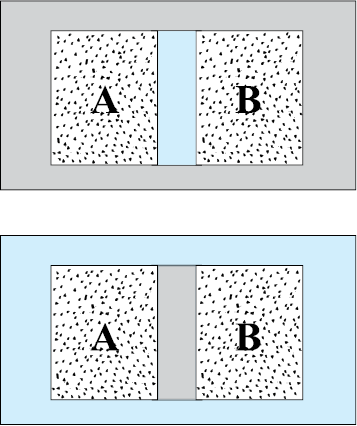
Fig. 12.1 (a) Systems A and B (two gases) separated by an adiabatic wall – an insulating wall that does not allow flow of heat. (b) The same systems A and B separated by a diathermic wall – a conducting wall that allows heat to flow from one to another. In this case, thermal equilibrium is attained in due course.

In general, whether or not a system is in a state of equilibrium depends on the surroundings and the nature of the wall that separates the system from the surroundings. Consider two gases A and B occupying two different containers. We know experimentally that pressure and volume of a given mass of gas can be chosen to be its two independent variables. Let the pressure and volume of the gases be (PA, VA) and (PB, VB) respectively. Suppose first that the two systems are put in proximity but are separated by an adiabatic wall – an insulating wall (can be movable) that does not allow flow of energy (heat) from one to another. The systems are insulated from the rest of the surroundings also by similar adiabatic walls. The situation is shown schematically in Fig. 12.1 (a). In this case, it is found that any possible pair of values (PA, VA) will be in equilibrium with any possible pair of values (PB, VB ). Next, suppose that the adiabatic wall is replaced by a diathermic wall – a conducting wall that allows energy flow (heat) from one to another. It is then found that the macroscopic variables of the systems A and B change spontaneously until both the systems attain equilibrium states. After that there is no change in their states. The situation is shown in Fig. 12.1(b). The pressure and volume variables of the two gases change to (PB ′, VB ′) and (PA ′, VA ′) such that the new states of A and B are in equilibrium with each other*. There is no more energy flow from one to another. We then say that the system A is in thermal equilibrium with the system B.

What characterises the situation of thermal equilibrium between two systems ? You can guess the answer from your experience. In thermal equilibrium, the temperatures of the two systems are equal. We shall see how does one arrive at the concept of temperature in thermodynamics? The Zeroth law of thermodynamics provides the clue.

12.3 Zeroth Law of Thermodynamics

Imagine two systems A and B, separated by an adiabatic wall, while each is in contact with a third system C, via a conducting wall [Fig. 12.2(a)]. The states of the systems (i.e., their macroscopic variables) will change until both A and B come to thermal equilibrium with C. After this is achieved, suppose that the adiabatic wall between A and B is replaced by a conducting wall and C is insulated from A and B by an adiabatic wall [Fig.12.2(b)]. It is found that the states of A and B change no further i.e. they are found to be in thermal equilibrium with each other. This observation forms the basis of the Zeroth Law of Thermodynamics, which states that ‘two systems in thermal equilibrium with a third system separately are in thermal equilibrium with each other’. R.H. Fowler formulated this law in 1931 long after the first and second Laws of thermodynamics were stated and so numbered.

The Zeroth Law clearly suggests that when two systems A and B, are in thermal equilibrium, there must be a physical quantity that has the same value for both. This thermodynamic variable whose value is equal for two systems in thermal equilibrium is called temperature (T ). Thus, if A and B are separately in equilibrium with C, TA = TC and TB = TC. This implies that TA = TB i.e. the systems A and B are also in thermal equilibrium.

We have arrived at the concept of temperature formally via the Zeroth Law. The next question is :how to assign numerical values to temperatures of different bodies ? In other words, how do we construct a scale of temperature ? Thermometry deals with this basic question to which we turn in the next section.

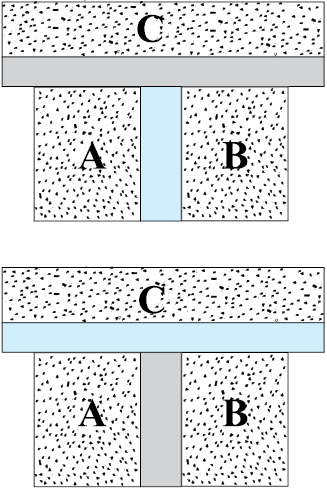
Fig. 12.2 (a) Systems A and B are separated by an adiabatic wall, while each is in contact with a third system C via a conducting wall. (b) The adiabatic wall between A and B is replaced by a conducting wall, while C is insulated from A and B by an adiabatic wall.

12.4 Heat, internal energy and work

The Zeroth Law of Thermodynamics led us to the concept of temperature that agrees with our commonsense notion. Temperature is a marker of the ‘hotness’ of a body. It determines the direction of flow of heat when two bodies are placed in thermal contact. Heat flows from the body at a higher temperature to the one at lower temperature. The flow stops when the temperatures equalise; the two bodies are then in thermal equilibrium. We saw in some detail how to construct temperature scales to assign temperatures to different bodies. We now describe the concepts of heat and other relevant quantities like internal energy and work.

The concept of internal energy of a system is not difficult to understand. We know that every bulk system consists of a large number of molecules. Internal energy is simply the sum of the kinetic energies and potential energies of these molecules. We remarked earlier that in thermodynamics, the kinetic energy of the system, as a whole, is not relevant. Internal energy is thus, the sum of molecular kinetic and potential energies in the frame of reference relative to which the centre of mass of the system is at rest. Thus, it includes only the (disordered) energy associated with the random motion of molecules of the system. We denote the internal energy of a system by U.

Though we have invoked the molecular picture to understand the meaning of internal energy, as far as thermodynamics is concerned, U is simply a macroscopic variable of the system. The important thing about internal energy is that it depends only on the state of the system, not on how that state was achieved. Internal energy U of a system is an example of a thermodynamic ‘state variable’ – its value depends only on the given state of the system, not on history i.e. not on the ‘path’ taken to arrive at that state. Thus, the internal energy of a given mass of gas depends on its state described by specific values of pressure, volume and temperature. It does not depend on how this state of the gas came about. Pressure, volume, temperature, and internal energy are thermodynamic state variables of the system (gas) (see section 12.7). If we neglect the small intermolecular forces in a gas, the internal energy of a gas is just the sum of kinetic energies associated with various random motions of its molecules. We will see in the next chapter that in a gas this motion is not only translational (i.e. motion from one point to another in the volume of the container); it also includes rotational and vibrational motion of the molecules (Fig. 12.3).

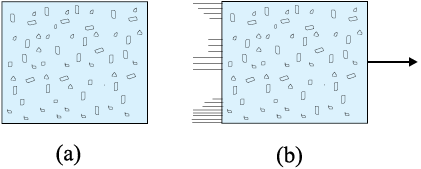
Fig. 12.3 (a) Internal energy U of a gas is the sum of the kinetic and potential energies of its molecules when the box is at rest. Kinetic energy due to various types of motion (translational, rotational, vibrational) is to be included in U. (b) If the same box is moving as a whole with some velocity, the kinetic energy of the box is not to be included in U.

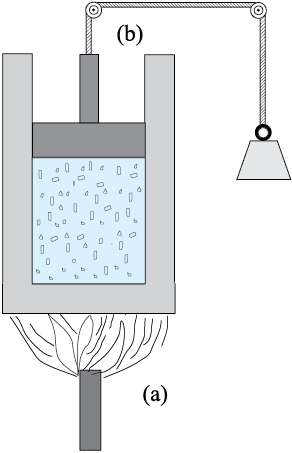
Fig. 12.4 Heat and work are two distinct modes of energy transfer to a system that results in change in its internal energy. (a) Heat is energy transfer due to temperature difference between the system and the surroundings. (b) Work is energy transfer brought about by means (e.g. moving the piston by raising or lowering some weight connected to it) that do not involve such a temperature difference.

What are the ways of changing internal energy of a system ? Consider again, for simplicity, the system to be a certain mass of gas contained in a cylinder with a movable piston as shown in Fig. 12.4. Experience shows there are two ways of changing the state of the gas (and hence its internal energy). One way is to put the cylinder in contact with a body at a higher temperature than that of the gas. The temperature difference will cause a flow of energy (heat) from the hotter body to the gas, thus increasing the internal energy of the gas. The other way is to push the piston down i.e. to do work on the system, which again results in increasing the internal energy of the gas. Of course, both these things could happen in the reverse direction. With surroundings at a lower temperature, heat would flow from the gas to the surroundings. Likewise, the gas could push the piston up and do work on the surroundings. In short, heat and work are two different modes of altering the state of a thermodynamic system and changing its internal energy.

The notion of heat should be carefully distinguished from the notion of internal energy. Heat is certainly energy, but it is the energy in transit. This is not just a play of words. The distinction is of basic significance. The state of a thermodynamic system is characterised by its internal energy, not heat. A statement like ‘a gas in a given state has a certain amount of heat’ is as meaningless as the statement that ‘a gas in a given state has a certain amount of work’. In contrast, ‘a gas in a given state has a certain amount of internal energy’ is a perfectly meaningful statement. Similarly, the statements ‘a certain amount of heat is supplied to the system’ or ‘a certain amount of work was done by the system’ are perfectly meaningful.

To summarise, heat and work in thermodynamics are not state variables. They are modes of energy transfer to a system resulting in change in its internal energy, which, as already mentioned, is a state variable.

In ordinary language, we often confuse heat with internal energy. The distinction between them is sometimes ignored in elementary physics books. For proper understanding of thermodynamics, however, the distinction is crucial.

12.5 First Law of Thermodynamics

We have seen that the internal energy U of a system can change through two modes of energy transfer : heat and work. Let

∆Q = Heat supplied to the system by the surroundings

∆W = Work done by the system on the surroundings

∆U = Change in internal energy of the system

The general principle of conservation of energy then implies that

∆Q = ∆U + ∆W (12.1)

i.e. the energy (∆Q) supplied to the system goes in partly to increase the internal energy of the system (∆U) and the rest in work on the environment (∆W). Equation (12.1) is known as the First Law of Thermodynamics. It is simply the general law of conservation of energy applied to any system in which the energy transfer from or to the surroundings is taken into account.

Let us put Eq. (12.1) in the alternative form

∆Q – ∆W = ∆U (12.2)

Now, the system may go from an initial state to the final state in a number of ways. For example, to change the state of a gas from (P1, V1) to (P2, V2), we can first change the volume of the gas from V1 to V2, keeping its pressure constant i.e. we can first go the state (P1, V2) and then change the pressure of the gas from P1 to P2, keeping volume constant, to take the gas to (P2, V2). Alternatively, we can first keep the volume constant and then keep the pressure constant. Since U is a state variable, ∆U depends only on the initial and final states and not on the path taken by the gas to go from one to the other. However, ∆Q and ∆W will, in general, depend on the path taken to go from the initial to final states. From the First Law of Thermodynamics, Eq. (12.2), it is clear that the combination ∆Q – ∆W, is however, path independent. This shows that if a system is taken through a process in which ∆U = 0 (for example, isothermal expansion of an ideal gas, see section 12.8),

∆Q = ∆W

i.e., heat supplied to the system is used up entirely by the system in doing work on the environment.

If the system is a gas in a cylinder with a movable piston, the gas in moving the piston does work. Since force is pressure times area, and area times displacement is volume, work done by the system against a constant pressure P is

∆W = P ∆V

where ∆V is the change in volume of the gas. Thus, for this case, Eq. (12.1) gives

∆Q = ∆U + P ∆V (12.3)

As an application of Eq. (12.3), consider the change in internal energy for 1 g of water when we go from its liquid to vapour phase. The measured latent heat of water is 2256 J/g. i.e., for 1 g of water ∆Q = 2256 J. At atmospheric pressure, 1 g of water has a volume 1 cm3 in liquid phase and 1671 cm3 in vapour phase.

Therefore,

∆W =P (Vg –Vl ) = 1.013 ×105 ×(1671×10–6) =169.2 J

Equation (12.3) then gives

∆U = 2256 – 169.2 = 2086.8 J

We see that most of the heat goes to increase the internal energy of water in transition from the liquid to the vapour phase.

12.6 Specific heat capacity

Suppose an amount of heat ∆Q supplied to a substance changes its temperature from T to T + ∆T. We define heat capacity of a substance (see Chapter 11) to be

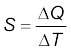(12.4)

We expect ∆Q and, therefore, heat capacity S to be proportional to the mass of the substance. Further, it could also depend on the temperature, i.e., a different amount of heat may be needed for a unit rise in temperature at different temperatures. To define a constant characteristic of the substance and independent of its amount, we divide S by the mass of the substance m in kg :

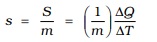 (12.5)

s is known as the specific heat capacity of the substance. It depends on the nature of the substance and its temperature. The unit of specific heat capacity is J kg–1 K–1.

If the amount of substance is specified in terms of moles µ (instead of mass m in kg ), we can define heat capacity per mole of the substance by

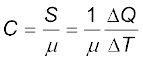(12.6)

C is known as molar specific heat capacity of the substance. Like s, C is independent of the amount of substance. C depends on the nature of the substance, its temperature and the conditions under which heat is supplied. The unit of C is J mo1–1 K–1. As we shall see later (in connection with specific heat capacity of gases), additional conditions may be needed to define C or s. The idea in defining C is that simple predictions can be made in regard to molar specific heat capacities.

Table 12.1 lists measured specific and molar heat capacities of solids at atmospheric pressure and ordinary room temperature.

We will see in Chapter 13 that predictions of specific heats of gases generally agree with experiment. We can use the same law of equipartition of energy that we use there to predict molar specific heat capacities of solids (See Section 13.5 and 13.6). Consider a solid of N atoms, each vibrating about its mean position. An oscillator in one dimension has average energy of 2 × ½ kBT = kBT. In three dimensions, the average energy is 3 kBT.
For a mole of a solid, the total energy is

U = 3 kBT × NA = 3 RT (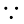kBT × NA = R)

Now, at constant pressure, ∆Q = ∆U + P ∆V ≅ ∆U, since for a solid ∆V is negligible. Therefore,

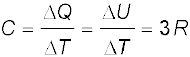(12.7)

Table 12.1 Specific and molar heat capacities of some solids at room temperature and atmospheric pressure

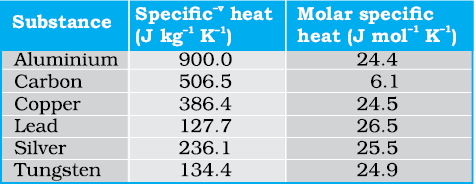
As Table 12.1 shows, the experimentally measured values which generally agrees with predicted value 3R at ordinary temperatures. (Carbon is an exception.) The agreement is known to break down at low temperatures.

Specific heat capacity of water

The old unit of heat was calorie. One calorie was earlier defined to be the amount of heat required to raise the temperature of 1g of water by 1°C. With more precise measurements, it was found that the specific heat of water varies slightly with temperature. Figure 12.5 shows this variation in the temperature range 0 to 100 °C.

 

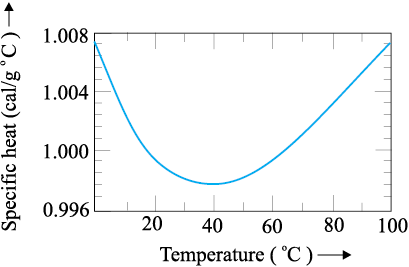
Fig. 12.5 Variation of specific heat capacity of water with temperature.

For a precise definition of calorie, it was, therefore, necessary to specify the unit temperature interval. One calorie is defined to be the amount of heat required to raise the temperature of 1g of water from 14.5 °C to 15.5°C. Since heat is just a form of energy, it is preferable to use the unit joule, J. In SI units, the specific heat capacity of water is 4186 J kg–1 K–1 i.e. 4.186 J g–1 K–1. The so called mechanical equivalent of heat defined as the amount of work needed to produce 1 cal of heat is in fact just a conversion factor between two different units of energy : calorie to joule. Since in SI units, we use the unit joule for heat, work or any other form of energy, the term mechanical equivalent is now superfluous and need not be used.

As already remarked, the specific heat capacity depends on the process or the conditions under which heat capacity transfer takes place. For gases, for example, we can define two specific heats : specific heat capacity at constant volume and specific heat capacity at constant pressure. For an ideal gas, we have a simple relation.

Cp – Cv = R (12.8)

where Cp and Cv are molar specific heat capacities of an ideal gas at constant pressure and volume respectively and R is the universal gas constant. To prove the relation, we begin with Eq. (12.3) for 1 mole of the gas :

∆Q = ∆U + P ∆V

If ∆Q is absorbed at constant volume, ∆V = 0

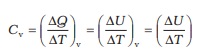 (12.9)

where the subscript v is dropped in the last step, since U of an ideal gas depends only on temperature. (The subscript denotes the quantity kept fixed.) If, on the other hand, ∆Q is absorbed at constant pressure,

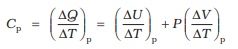 (12.10)

The subscript p can be dropped from the first term since U of an ideal gas depends only on T. Now, for a mole of an ideal gas

PV = RT

which gives

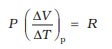 (12.11)

Equations (12.9) to (12.11) give the desired relation, Eq. (12.8).

12.7 Thermodynamic state variables and Equation of State

Every equilibrium state of a thermodynamic system is completely described by specific values of some macroscopic variables, also called state variables. For example, an equilibrium state of a gas is completely specified by the values of pressure, volume, temperature, and mass (and composition if there is a mixture of gases). A thermodynamic system is not always in equilibrium. For example, a gas allowed to expand freely against vacuum is not an equilibrium state [Fig. 12.6(a)]. During the rapid expansion, pressure of the gas may not be uniform throughout. Similarly, a mixture of gases undergoing an explosive chemical reaction (e.g. a mixture of petrol vapour and air when ignited by a spark) is not an equilibrium state; again its temperature and pressure are not uniform [Fig. 12.6(b)]. Eventually, the gas attains a uniform temperature and pressure and comes to thermal and mechanical equilibrium with its surroundings.

 

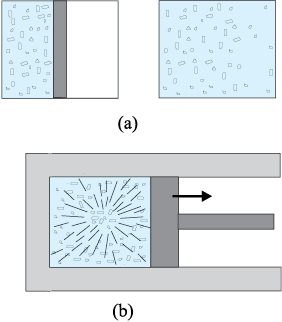
Fig. 12.6 (a) The partition in the box is suddenly removed leading to free expansion of the gas. (b) A mixture of gases undergoing an explosive chemical reaction. In both situations, the gas is not in equilibrium and cannot be described by state variables.

In short, thermodynamic state variables describe equilibrium states of systems. The various state variables are not necessarily independent. The connection between the state variables is called the equation of state. For example, for an ideal gas, the equation of state is the ideal gas relation

P V = µ R T

For a fixed amount of the gas i.e. given µ, there are thus, only two independent variables, say P and V or T and V. The pressure-volume curve for a fixed temperature is called an isotherm. Real gases may have more complicated equations of state.

The thermodynamic state variables are of two kinds: extensive and intensive. Extensive variables indicate the ‘size’ of the system. Intensive variables such as pressure and temperature do not. To decide which variable is extensive and which intensive, think of a relevant system in equilibrium, and imagine that it is divided into two equal parts. The variables that remain unchanged for each part are intensive. The variables whose values get halved in each part are extensive. It is easily seen, for example, that internal energy U, volume V, total mass M are extensive variables. Pressure P, temperature T, and density ρ are intensive variables. It is a good practice to check the consistency of thermodynamic equations using this classification of variables. For example, in the equation

∆Q = ∆U + P ∆V

quantities on both sides are extensive*. (The product of an intensive variable like P and

• Chapters
• Q.Ans