Table of Contents
Chapter 4
Determinants
 All Mathematical truths are relative and conditional. — C.P. Steinmetz
All Mathematical truths are relative and conditional. — C.P. Steinmetz 
4.1 Introduction
In the previous chapter, we have studied about matrices and algebra of matrices. We have also learnt that a system of algebraic equations can be expressed in the form of matrices. This means, a system of linear equations like

P.S. Laplace
(1749-1827)
a1 x + b1 y = c1
a2 x + b2 y = c2
can be represented as 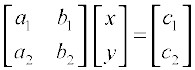 . Now, this system of equations has a unique solution or not, is determined by the number a1 b2 – a2 b1. (Recall that if
. Now, this system of equations has a unique solution or not, is determined by the number a1 b2 – a2 b1. (Recall that if 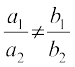 or, a1 b2 – a2 b1 ≠ 0, then the system of linear equations has a unique solution). The number a1 b2 – a2 b1 which determines uniqueness of solution is associated with the matrix
or, a1 b2 – a2 b1 ≠ 0, then the system of linear equations has a unique solution). The number a1 b2 – a2 b1 which determines uniqueness of solution is associated with the matrix 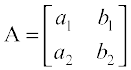 and is called the determinant of A or det A. Determinants have wide applications in Engineering, Science, Economics, Social Science, etc.
and is called the determinant of A or det A. Determinants have wide applications in Engineering, Science, Economics, Social Science, etc.
In this chapter, we shall study determinants up to order three only with real entries. Also, we will study various properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle, adjoint and inverse of a square matrix, consistency and inconsistency of system of linear equations and solution of linear equations in two or three variables using inverse of a matrix.
4.2 Determinant
To every square matrix A = [aij] of order n, we can associate a number (real or complex) called determinant of the square matrix A, where aij = (i, j)th element of A. This may be thought of as a function which associates each square matrix with a unique number (real or complex). If M is the set of square matrices, K is the set of numbers (real or complex) and f : M → K is defined by f(A) = k, where A ∈ M and
k ∈ K, then f(A) is called the determinant of A. It is also denoted by |A| or det A or ∆.
If A =  , then determinant of A is written as |A| =
, then determinant of A is written as |A| =  = det (A)
= det (A)
Remarks
(i) For matrix A, |A| is read as determinant of A and not modulus of A.
(ii) Only square matrices have determinants.
4.2.1 Determinant of a matrix of order one
Let A = [a] be the matrix of order 1, then determinant of A is defined to be equal to a
4.2.2 Determinant of a matrix of order two
Let A = 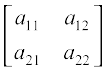 be a matrix of order 2 × 2,
be a matrix of order 2 × 2,
then the determinant of A is defined as:
det (A) = |A| = ∆ = 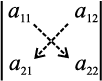 = a11a22 – a21a12
= a11a22 – a21a12
Example 1 Evaluate 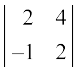 .
.
Solution We have 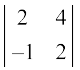 = 2(2) – 4(–1) = 4 + 4 = 8.
= 2(2) – 4(–1) = 4 + 4 = 8.
Example 2 Evaluate 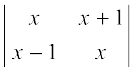
Solution We have
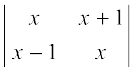 = x (x) – (x + 1) (x – 1) = x2 – (x2 – 1) = x2 – x2 + 1 = 1
= x (x) – (x + 1) (x – 1) = x2 – (x2 – 1) = x2 – x2 + 1 = 1
4.2.3 Determinant of a matrix of order 3 × 3
Determinant of a matrix of order three can be determined by expressing it in terms of second order determinants. This is known as expansion of a determinant along
a row (or a column). There are six ways of expanding a determinant of order
3 corresponding to each of three rows (R1, R2 and R3) and three columns (C1, C2 and C3) giving the same value as shown below.
Consider the determinant of square matrix A = [aij]3 × 3
i.e., | A | = 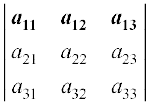
Expansion along first Row (R1)
Step 1 Multiply first element a11 of R1 by (–1)(1 + 1) [(–1)sum of suffixes in a11] and with the second order determinant obtained by deleting the elements of first row (R1) and first column (C1) of | A | as a11 lies in R1 and C1,
i.e., (–1)1 + 1 a11 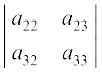
Step 2 Multiply 2nd element a12 of R1 by (–1)1 + 2 [(–1)sum of suffixes in a12] and the second order determinant obtained by deleting elements of first row (R1) and 2nd column (C2) of | A | as a12 lies in R1 and C2,
i.e., (–1)1 + 2 a12 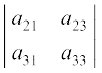
Step 3 Multiply third element a13 of R1 by (–1)1 + 3 [(–1)sum of suffixes in a13] and the second order determinant obtained by deleting elements of first row (R1) and third column (C3) of | A | as a13 lies in R1 and C3,
i.e., (–1)1 + 3 a13 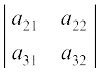
Step 4 Now the expansion of determinant of A, that is, | A | written as sum of all three terms obtained in steps 1, 2 and 3 above is given by
det A = |A| = (–1)1 + 1 a11 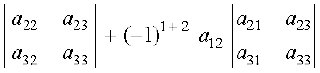
+ 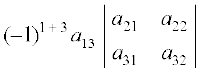
or |A| = a11 (a22 a33 – a32 a23) – a12 (a21 a33 – a31 a23)
+ a13 (a21 a32 – a31 a22)
= a11 a22 a33 – a11 a32 a23 – a12 a21 a33 + a12 a31 a23 + a13 a21 a32
– a13 a31 a22 ... (1)
Note We shall apply all four steps together.
Expansion along second row (R2)
| A | = 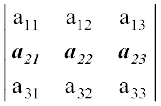
Expanding along R2, we get
| A | = 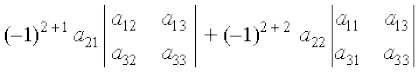
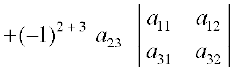
= – a21 (a12 a33 – a32 a13) + a22 (a11 a33 – a31 a13)
– a23 (a11 a32 – a31 a12)
| A | = – a21 a12 a33 + a21 a32 a13 + a22 a11 a33 – a22 a31 a13 – a23 a11 a32
+ a23 a31 a12
= a11 a22 a33 – a11 a23 a32 – a12 a21 a33 + a12 a23 a31 + a13 a21 a32
– a13 a31 a22 ... (2)
Expansion along first Column (C1)
| A | = 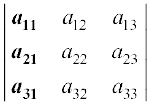
By expanding along C1, we get
| A | = 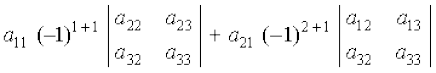
+ 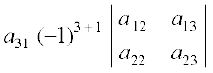
= a11 (a22 a33 – a23 a32) – a21 (a12 a33 – a13 a32) + a31 (a12 a23 – a13 a22)
| A | = a11 a22 a33 – a11 a23 a32 – a21 a12 a33 + a21 a13 a32 + a31 a12 a23
– a31 a13 a22
= a11 a22 a33 – a11 a23 a32 – a12 a21 a33 + a12 a23 a31 + a13 a21 a32
– a13 a31 a22 ... (3)
Clearly, values of |A| in (1), (2) and (3) are equal. It is left as an exercise to the reader to verify that the values of |A| by expanding along R3, C2 and C3 are equal to the value of |A| obtained in (1), (2) or (3).
Hence, expanding a determinant along any row or column gives same value.
Remarks
(i) For easier calculations, we shall expand the determinant along that row or column which contains maximum number of zeros.
(ii) While expanding, instead of multiplying by (–1)i + j, we can multiply by +1 or –1 according as (i + j) is even or odd.
(iii) Let A = 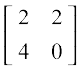 and B =
and B = 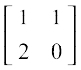 . Then, it is easy to verify that A = 2B. Also |A| = 0 – 8 = – 8 and |B| = 0 – 2 = – 2.
. Then, it is easy to verify that A = 2B. Also |A| = 0 – 8 = – 8 and |B| = 0 – 2 = – 2.
Observe that, |A| = 4(– 2) = 22|B| or |A| = 2n|B|, where n = 2 is the order of square matrices A and B.
In general, if A = kB where A and B are square matrices of order n, then | A| = kn | B |, where n = 1, 2, 3
Example 3 Evaluate the determinant ∆ = 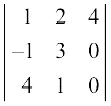 .
.
Solution Note that in the third column, two entries are zero. So expanding along third column (C3), we get
∆ = 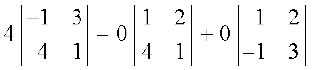
= 4 (–1 – 12) – 0 + 0 = – 52
Example 4 Evaluate ∆ = 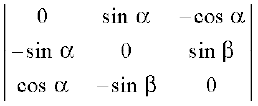 .
.
Solution Expanding along R1, we get
∆ = 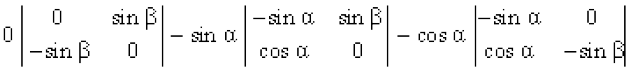
= 0 – sin α (0 – sin β cos α) – cos α (sin α sin β – 0)
= sin α sin β cos α – cos α sin α sin β = 0
Example 5 Find values of x for which 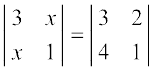 .
.
Solution We have 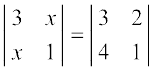
i.e. 3 – x2 = 3 – 8
i.e. x2 = 8
Hence x = 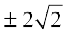
Exercise 4.1
Evaluate the determinants in Exercises 1 and 2.
1. 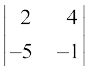
2. (i) 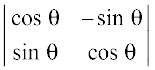 (ii)
(ii) 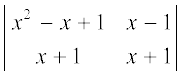
3. If A = 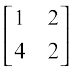 , then show that | 2A | = 4 | A |
, then show that | 2A | = 4 | A |
4. If A =  , then show that | 3 A | = 27 | A |
, then show that | 3 A | = 27 | A |
5. Evaluate the determinants
(i) 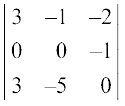 (ii)
(ii) 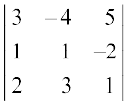
(iii) 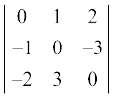 (iv)
(iv) 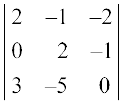
6. If A = 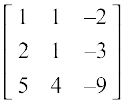 , find | A |
, find | A |
7. Find values of x, if
(i) 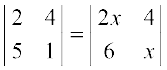 (ii)
(ii) 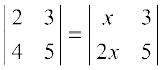
8. If 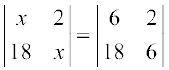 , then x is equal to
, then x is equal to
(A) 6 (B) ± 6 (C) – 6 (D) 0
4.3 Properties of Determinants
In the previous section, we have learnt how to expand the determinants. In this section, we will study some properties of determinants which simplifies its evaluation by obtaining maximum number of zeros in a row or a column. These properties are true for determinants of any order. However, we shall restrict ourselves upto determinants of order 3 only.
Property 1 The value of the determinant remains unchanged if its rows and columns are interchanged.
Verification Let ∆ = 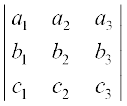
Expanding along first row, we get
∆ = 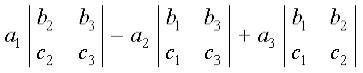
= a1 (b2 c3 – b3 c2) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
By interchanging the rows and columns of ∆, we get the determinant
∆1 = 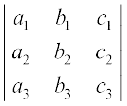
Expanding ∆1 along first column, we get
∆1 = a1 (b2 c3 – c2 b3) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
Hence ∆ = ∆1
Remark It follows from above property that if A is a square matrix, then
det (A) = det (A′), where A′ = transpose of A.
Note If Ri = ith row and Ci = ith column, then for interchange of row and columns, we will symbolically write Ci ↔ Ri
Let us verify the above property by example.
Example 6 Verify Property 1 for ∆ = 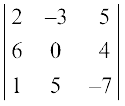
Solution Expanding the determinant along first row, we have
∆ = 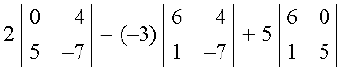
= 2 (0 – 20) + 3 (– 42 – 4) + 5 (30 – 0)
= – 40 – 138 + 150 = – 28
By interchanging rows and columns, we get
∆1 = 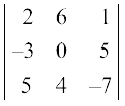 (Expanding along first column)
(Expanding along first column)
= 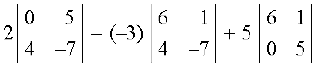
= 2 (0 – 20) + 3 (– 42 – 4) + 5 (30 – 0)
= – 40 – 138 + 150 = – 28
Clearly ∆ = ∆1
Hence, Property 1 is verified.
Property 2 If any two rows (or columns) of a determinant are interchanged, then sign of determinant changes.
Verification Let ∆ = 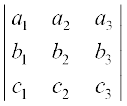
Expanding along first row, we get
∆ = a1 (b2 c3 – b3 c2) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
Interchanging first and third rows, the new determinant obtained is given by
∆1 = 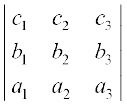
Expanding along third row, we get
∆1 = a1 (c2 b3 – b2 c3) – a2 (c1 b3 – c3 b1) + a3 (b2 c1 – b1 c2)
= – [a1 (b2 c3 – b3 c2) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)]
Clearly ∆1 = – ∆
Similarly, we can verify the result by interchanging any two columns.
Note We can denote the interchange of rows by Ri ↔ Rj and interchange of columns by Ci ↔ Cj.
Example 7 Verify Property 2 for ∆ = 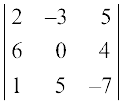 .
.
Solution ∆ = 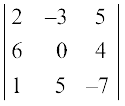 = – 28 (See Example 6)
= – 28 (See Example 6)
Interchanging rows R2 and R3 i.e., R2 ↔ R3, we have
∆1 = 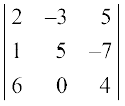
Expanding the determinant ∆1 along first row, we have
∆1 = 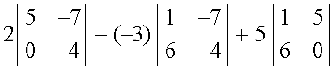
= 2 (20 – 0) + 3 (4 + 42) + 5 (0 – 30)
= 40 + 138 – 150 = 28
Clearly ∆1 = – ∆
Hence, Property 2 is verified.
Property 3 If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then value of determinant is zero.
Proof If we interchange the identical rows (or columns) of the determinant ∆, then ∆ does not change. However, by Property 2, it follows that ∆ has changed its sign
Therefore ∆ = – ∆
or ∆ = 0
Let us verify the above property by an example.
Example 8 Evaluate ∆ = 
Solution Expanding along first row, we get
∆ = 3 (6 – 6) – 2 (6 – 9) + 3 (4 – 6)
= 0 – 2 (–3) + 3 (–2) = 6 – 6 = 0
Here R1 and R3 are identical.
Property 4 If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.
Verification Let ∆ = 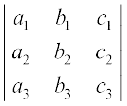
and ∆1 be the determinant obtained by multiplying the elements of the first row by k.
Then
∆1 = 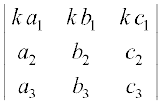
Expanding along first row, we get
∆1 = k a1 (b2 c3 – b3 c2) – k b1 (a2 c3 – c2 a3) + k c1 (a2 b3 – b2 a3)
= k [a1 (b2 c3 – b3 c2) – b1 (a2 c3 – c2 a3) + c1 (a2 b3 – b2 a3)]
= k ∆
Hence 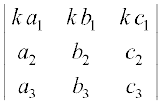 = k
= k 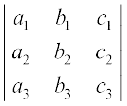
Remarks
(i) By this property, we can take out any common factor from any one row or any one column of a given determinant.
(ii) If corresponding elements of any two rows (or columns) of a determinant are proportional (in the same ratio), then its value is zero. For example
∆ = 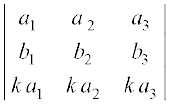 = 0 (rows R1 and R2 are proportional)
= 0 (rows R1 and R2 are proportional)
Example 9 Evaluate 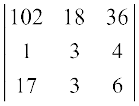
Solution Note that 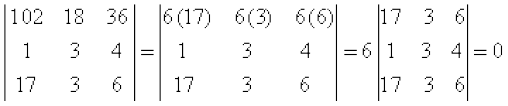
(Using Properties 3 and 4)
Property 5 If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants.
For example,
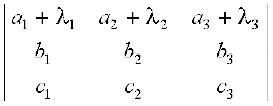 =
= 
Verification L.H.S. = 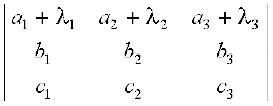
Expanding the determinants along the first row, we get
∆ = (a1 + λ1) (b2 c3 – c2 b3) – (a2 + λ2) (b1 c3 – b3 c1)
+ (a3 + λ3) (b1 c2 – b2 c1)
= a1 (b2 c3 – c2 b3) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
+ λ1 (b2 c3 – c2 b3) – λ2 (b1 c3 – b3 c1) + λ3 (b1 c2 – b2 c1)
(by rearranging terms)
=  = R.H.S.
= R.H.S.
Similarly, we may verify Property 5 for other rows or columns.
Example 10 Show that 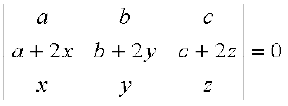
Solution We have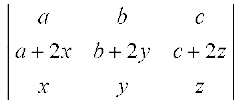 =
= 
(by Property 5)
= 0 + 0 = 0 (Using Property 3 and Property 4)
Property 6 If, to each element of any row or column of a determinant, the equimultiples of corresponding elements of other row (or column) are added, then value of determinant remains the same, i.e., the value of determinant remain same if we apply the operation Ri → Ri + kRj or Ci → Ci + kCj.
Verification
Let ∆ = 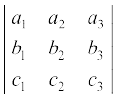 and ∆1 =
and ∆1 = 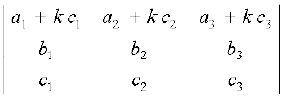 ,
,
where ∆1 is obtained by the operation R1 → R1 + kR3 .
Here, we have multiplied the elements of the third row (R3) by a constant k and added them to the corresponding elements of the first row (R1).
Symbolically, we write this operation as R1 → R1 + k R3.
Now, again
∆1 =  (Using Property 5)
(Using Property 5)
= ∆ + 0 (since R1 and R3 are proportional)
Hence ∆ = ∆1
Remarks
(i) If ∆1 is the determinant obtained by applying Ri → kRi or Ci → kCi to the determinant ∆, then ∆1 = k∆.
(ii) If more than one operation like Ri → Ri + kRj is done in one step, care should be taken to see that a row that is affected in one operation should not be used in another operation. A similar remark applies to column operations.
Example 11 Prove that 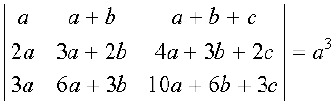 .
.
Solution Applying operations R2 → R2 – 2R1 and R3 → R3 – 3R1 to the given determinant ∆, we have
∆ = 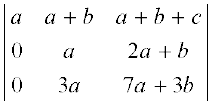
Now applying R3 → R3 – 3R2 , we get
∆ = 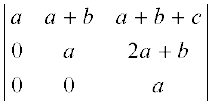
Expanding along C1, we obtain
∆ = 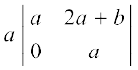 + 0 + 0
+ 0 + 0
= a (a2 – 0) = a (a2) = a3
Example 12 Without expanding, prove that
∆ = 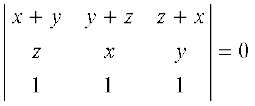
Solution Applying R1 → R1 + R2 to ∆, we get
∆ = 
Since the elements of R1 and R3 are proportional, ∆ = 0.
Example 13 Evaluate
∆ = 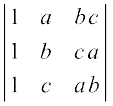
Solution Applying R2 → R2 – R1 and R3 → R3 – R1, we get
∆ = 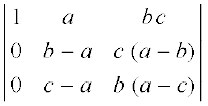
Taking factors (b – a) and (c – a) common from R2 and R3, respectively, we get
∆ = 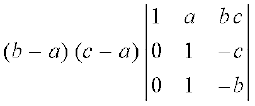
= (b – a) (c – a) [(– b + c)] (Expanding along first column)
= (a – b) (b – c) (c – a)
Example 14 Prove that 
Solution Let ∆ = 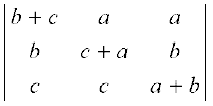
Applying R1 → R1 – R2 – R3 to ∆, we get
∆ = 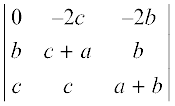
Expanding along R1, we obtain
∆ = 
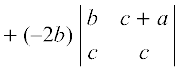
= 2 c (a b + b2 – bc) – 2 b (b c – c2 – ac)
= 2 a b c + 2 cb2 – 2 bc2 – 2 b2c + 2 bc2 + 2 abc
= 4 abc
Example 15 If x, y, z are different and 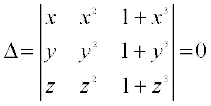 , then
, then
show that 1 + xyz = 0
Solution We have
∆ = 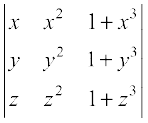
=  (Using Property 5)
(Using Property 5)
=  (Using C3↔C2 and then C1 ↔ C2)
(Using C3↔C2 and then C1 ↔ C2)
= 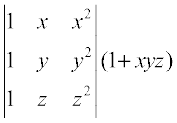
= 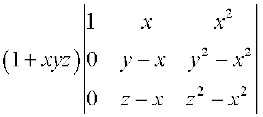 (Using R2→R2–R1 and R3 → R3–R1)
(Using R2→R2–R1 and R3 → R3–R1)
Taking out common factor (y – x) from R2 and (z – x) from R3, we get
∆ = 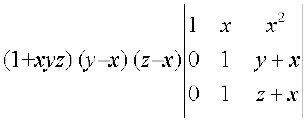
= (1 + xyz) (y – x) (z – x) (z – y) (on expanding along C1)
Since ∆ = 0 and x, y, z are all different, i.e., x – y ≠ 0, y – z ≠ 0, z – x ≠ 0, we get 1 + xyz = 0
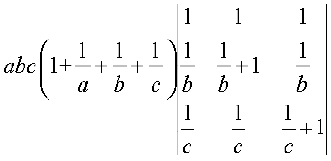
Example 16 Show that
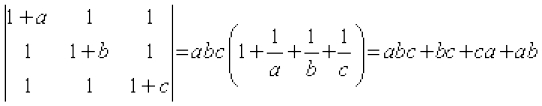
Solution Taking out factors a,b,c common from R1, R2 and R3, we get
L.H.S. = 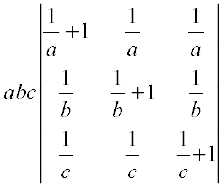
Applying R1→ R1 + R2 + R3, we have
∆ = 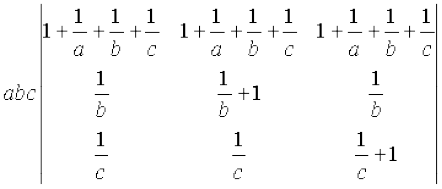
= 
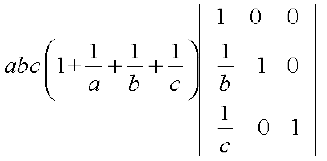
Now applying C2 → C2 – C1, C3 → C3 – C1, we get
∆ = 
= 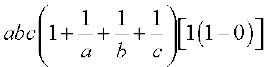
= 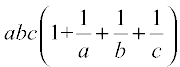 = abc + bc + ca + ab = R.H.S.
= abc + bc + ca + ab = R.H.S.
Note Alternately try by applying C1 → C1 – C2 and C3 → C3 – C2, then apply
C1 → C1 – a C3.
Exercise 4.2
Using the property of determinants and without expanding in Exercises 1 to 7, prove that:
1. 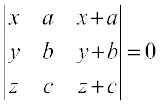
2. 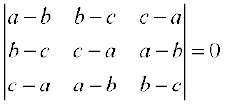
3. 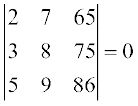
4. 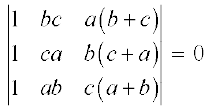
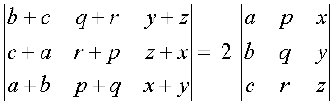
5. 
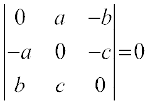
6. 
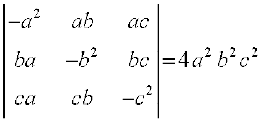
7. 
By using properties of determinants, in Exercises 8 to 14, show that:
8. (i) 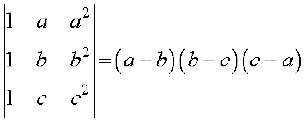
(ii) 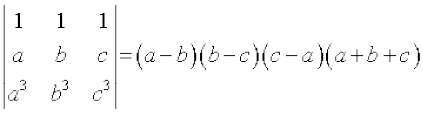
9. 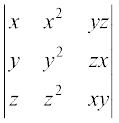 = (x – y) (y – z) (z – x) (xy + yz + zx)
= (x – y) (y – z) (z – x) (xy + yz + zx)
10. (i) 
(ii) 
11. (i) 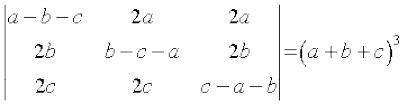
(ii) 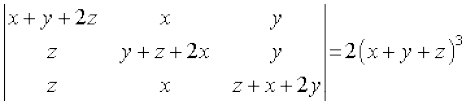
12. 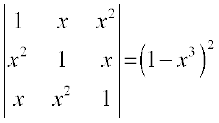
13. 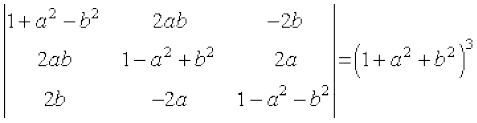
14. 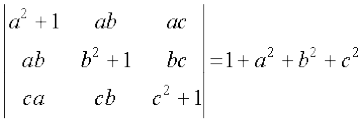
Choose the correct answer in Exercises 15 and 16.
15. Let A be a square matrix of order 3 × 3, then |kA| is equal to
(A) k|A| (B) k2|A| (C) k3|A| (D) 3k|A|
16. Which of the following is correct
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
4.4 Area of a Triangle
In earlier classes, we have studied that the area of a triangle whose vertices are
(x1, y1), (x2, y2) and (x3, y3), is given by the expression  [x1(y2–y3) + x2 (y3–y1) +
[x1(y2–y3) + x2 (y3–y1) +
x3 (y1–y2)]. Now this expression can be written in the form of a determinant as
∆ = 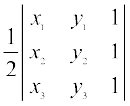 ... (1)
... (1)
Remarks
(i) Since area is a positive quantity, we always take the absolute value of the determinant in (1).
(ii) If area is given, use both positive and negative values of the determinant for calculation.
(iii) The area of the triangle formed by three collinear points is zero.
Example 17 Find the area of the triangle whose vertices are (3, 8), (– 4, 2) and (5, 1).
Solution The area of triangle is given by
∆ = 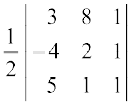
= 
= 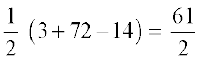
Example 18 Find the equation of the line joining A(1, 3) and B (0, 0) using determinants and find k if D(k, 0) is a point such that area of triangle ABD is 3sq units.
Solution Let P (x, y) be any point on AB. Then, area of triangle ABP is zero (Why?). So
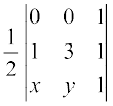 = 0
= 0
This gives 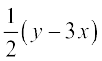 = 0 or y = 3x,
= 0 or y = 3x,
which is the equation of required line AB.
Also, since the area of the triangle ABD is 3 sq. units, we have
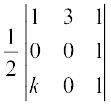 = ± 3
= ± 3
This gives, 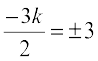 , i.e., k =
, i.e., k = 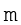 2.
2.
Exercise 4.3
1. Find area of the triangle with vertices at the point given in each of the following :
(i) (1, 0), (6, 0), (4, 3) (ii) (2, 7), (1, 1), (10, 8)
(iii) (–2, –3), (3, 2), (–1, –8)
2. Show that points
A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
3. Find values of k if area of triangle is 4 sq. units and vertices are
(i) (k, 0), (4, 0), (0, 2) (ii) (–2, 0), (0, 4), (0, k)
4. (i) Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants.
5. If area of triangle is 35 sq units with vertices (2, – 6), (5, 4) and (k, 4). Then k is
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2
4.5 Minors and Cofactors
In this section, we will learn to write the expansion of a determinant in compact form using minors and cofactors.
Definition 1 Minor of an element aij of a determinant is the determinant obtained by deleting its ith row and jth column in which element aij lies. Minor of an element aij is denoted by Mij.
Remark Minor of an element of a determinant of order n(n ≥ 2) is a determinant of order n – 1.
Example 19 Find the minor of element 6 in the determinant 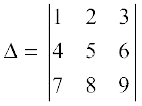
Solution Since 6 lies in the second row and third column, its minor M23 is given by
M23 = 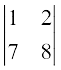 = 8 – 14 = – 6 (obtained by deleting R2 and C3 in ∆).
= 8 – 14 = – 6 (obtained by deleting R2 and C3 in ∆).
Definition 2 Cofactor of an element aij, denoted by Aij is defined by
Aij = (–1)i + j Mij, where Mij is minor of aij.
Example 20 Find minors and cofactors of all the elements of the determinant 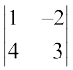
Solution Minor of the element aij is Mij
Here a11 = 1. So M11 = Minor of a11= 3
M12 = Minor of the element a12 = 4
M21 = Minor of the element a21 = –2
M22 = Minor of the element a22 = 1
Now, cofactor of aij is Aij. So
A11 = (–1)1 + 1 M11 = (–1)2 (3) = 3
A12 = (–1)1 + 2 M12 = (–1)3 (4) = – 4
A21 = (–1)2 + 1 M21 = (–1)3 (–2) = 2
A22 = (–1)2 + 2 M22 = (–1)4 (1) = 1
Example 21 Find minors and cofactors of the elements a11, a21 in the determinant
∆ = 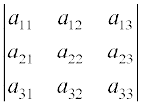
Solution By definition of minors and cofactors, we have
Minor of a11 = M11 = 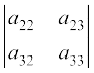 = a22 a33– a23 a32
= a22 a33– a23 a32
Cofactor of a11 = A11 = (–1)1+1 M11 = a22 a33 – a23 a32
Minor of a21 = M21 = 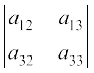 = a12 a33 – a13 a32
= a12 a33 – a13 a32
Cofactor of a21 = A21 = (–1)2+1 M21 = (–1) (a12 a33 – a13 a32) = – a12 a33 + a13 a32
Remark Expanding the determinant ∆, in Example 21, along R1, we have
∆ = (–1)1+1 a11 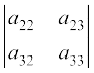 + (–1)1+2 a12
+ (–1)1+2 a12 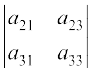 + (–1)1+3 a13
+ (–1)1+3 a13 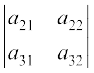
= a11 A11 + a12 A12 + a13 A13, where Aij is cofactor of aij
= sum of product of elements of R1 with their corresponding cofactors
Similarly, ∆ can be calculated by other five ways of expansion that is along R2, R3, C1, C2 and C3.
Hence ∆ = sum of the product of elements of any row (or column) with their corresponding cofactors.
Note If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero. For example,
∆ = a11 A21 + a12 A22 + a13 A23
= a11 (–1)1+1 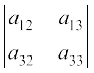 + a12 (–1)1+2
+ a12 (–1)1+2 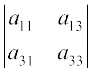 + a13 (–1)1+3
+ a13 (–1)1+3 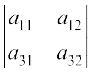
= 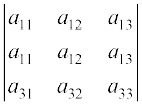 = 0 (since R1 and R2 are identical)
= 0 (since R1 and R2 are identical)
Similarly, we can try for other rows and columns.
Example 22 Find minors and cofactors of the elements of the determinant
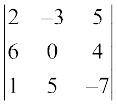 and verify that a11 A31 + a12 A32 + a13 A33= 0
and verify that a11 A31 + a12 A32 + a13 A33= 0
Solution We have M11 =  = 0 –20 = –20; A11 = (–1)1+1 (–20) = –20
= 0 –20 = –20; A11 = (–1)1+1 (–20) = –20
M12 = 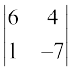 = – 42 – 4 = – 46; A12 = (–1)1+2 (– 46) = 46
= – 42 – 4 = – 46; A12 = (–1)1+2 (– 46) = 46
M13 = 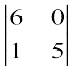 = 30 – 0 = 30; A13 = (–1)1+3 (30) = 30
= 30 – 0 = 30; A13 = (–1)1+3 (30) = 30
M21 = 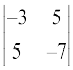 = 21 – 25 = – 4; A21 = (–1)2+1 (– 4) = 4
= 21 – 25 = – 4; A21 = (–1)2+1 (– 4) = 4
M22 = 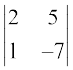 = –14 – 5 = –19; A22 = (–1)2+2 (–19) = –19
= –14 – 5 = –19; A22 = (–1)2+2 (–19) = –19
M23 = 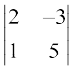 = 10 + 3 = 13; A23 = (–1)2+3 (13) = –13
= 10 + 3 = 13; A23 = (–1)2+3 (13) = –13
M31 = 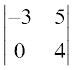 = –12 – 0 = –12; A31 = (–1)3+1 (–12) = –12
= –12 – 0 = –12; A31 = (–1)3+1 (–12) = –12
M32 = 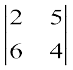 = 8 – 30 = –22; A32 = (–1)3+2 (–22) = 22
= 8 – 30 = –22; A32 = (–1)3+2 (–22) = 22
and M33 = 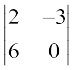 = 0 + 18 = 18; A33 = (–1)3+3 (18) = 18
= 0 + 18 = 18; A33 = (–1)3+3 (18) = 18
Now a11 = 2, a12 = –3, a13 = 5; A31 = –12, A32 = 22, A33 = 18
So a11 A31 + a12 A32 + a13 A33
= 2 (–12) + (–3) (22) + 5 (18) = –24 – 66 + 90 = 0
Exercise 4.4
Write Minors and Cofactors of the elements of following determinants:
1. (i) 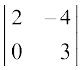 (ii)
(ii) 
2. (i)  (ii)
(ii) 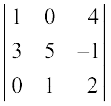
3. Using Cofactors of elements of second row, evaluate ∆ = 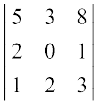 .
.
4. Using Cofactors of elements of third column, evaluate ∆ = 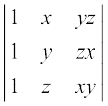 .
.
5. If ∆ = 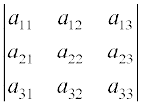 and Aij is Cofactors of aij, then value of ∆ is given by
and Aij is Cofactors of aij, then value of ∆ is given by
(A) a11 A31+ a12 A32 + a13 A33 (B) a11 A11+ a12 A21 + a13 A31
(C) a21 A11+ a22 A12 + a23 A13 (D) a11 A11+ a21 A21 + a31 A31
4.6 Adjoint and Inverse of a Matrix
In the previous chapter, we have studied inverse of a matrix. In this section, we shall discuss the condition for existence of inverse of a matrix.
To find inverse of a matrix A, i.e., A–1 we shall first define adjoint of a matrix.
4.6.1 Adjoint of a matrix
Definition 3 The adjoint of a square matrix A = [aij]n × n is defined as the transpose of the matrix [Aij]n × n, where Aij is the cofactor of the element aij. Adjoint of the matrix A is denoted by adj A.
Let 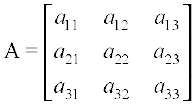
Then 
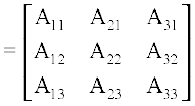
Example 23 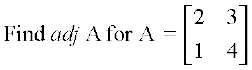
Solution We have A11 = 4, A12 = –1, A21 = –3, A22 = 2
Hence adj A = 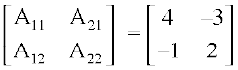
Remark For a square matrix of order 2, given by
A = 
The adj A can also be obtained by interchanging a11 and a22 and by changing signs of a12 and a21, i.e.,
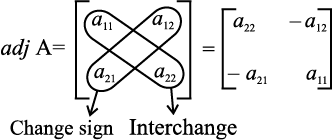
We state the following theorem without proof.
Theorem 1 If A be any given square matrix of order n, then
A(adj A) = (adj A) A =  ,
,
where I is the identity matrix of order n
Verification
Let A = 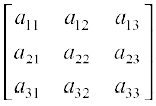 , then adj A =
, then adj A = 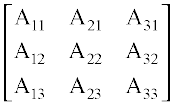
Since sum of product of elements of a row (or a column) with corresponding cofactors is equal to |A| and otherwise zero, we have
A (adj A) = 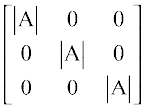 =
= 
 =
=  I
I
Similarly, we can show (adj A) A =  I
I
Hence A (adj A) = (adj A) A =  I
I
Definition 4 A square matrix A is said to be singular if  = 0.
= 0.
For example, the determinant of matrix A =  is zero
is zero
Hence A is a singular matrix.
Definition 5 A square matrix A is said to be non-singular if  ≠ 0
≠ 0
Let A =  . Then
. Then  =
= 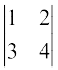 = 4 – 6 = – 2 ≠ 0.
= 4 – 6 = – 2 ≠ 0.
Hence A is a nonsingular matrix
We state the following theorems without proof.
Theorem 2 If A and B are nonsingular matrices of the same order, then AB and BA are also nonsingular matrices of the same order.
Theorem 3 The determinant of the product of matrices is equal to product of their respective determinants, that is,  =
= 
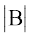 , where A and B are square matrices of the same order
, where A and B are square matrices of the same order
Remark We know that (adj A) A =  I =
I = 
Writing determinants of matrices on both sides, we have
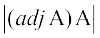 =
= 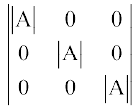
i.e. |(adj A)| |A| =  (Why?)
(Why?)
i.e. |(adj A)| |A| = |A|3 (1)
i.e. |(adj A)| = |A|2
In general, if A is a square matrix of order n, then |adj(A)| = |A|n – 1.
Theorem 4 A square matrix A is invertible if and only if A is nonsingular matrix.
Proof Let A be invertible matrix of order n and I be the identity matrix of order n.
Then, there exists a square matrix B of order n such that AB = BA = I
Now AB = I. So  =
=  or
or 
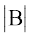 = 1
= 1 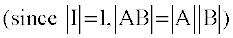
This gives  ≠ 0. Hence A is nonsingular.
≠ 0. Hence A is nonsingular.
Conversely, let A be nonsingular. Then  ≠ 0
≠ 0
Now A (adj A) = (adj A) A =  I (Theorem 1)
I (Theorem 1)
or A 
or AB = BA = I, where B = 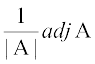
Thus A is invertible and A–1 = 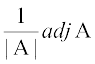
Example 24 If A =  , then verify that A adj A = |A| I. Also find A–1.
, then verify that A adj A = |A| I. Also find A–1.
Solution We have  = 1 (16 – 9) –3 (4 – 3) + 3 (3 – 4) = 1 ≠ 0
= 1 (16 – 9) –3 (4 – 3) + 3 (3 – 4) = 1 ≠ 0
Now A11 = 7, A12 = –1, A13 = –1, A21 = –3, A22 = 1, A23 = 0, A31 = –3, A32 = 0, A33 = 1
Therefore adj A = 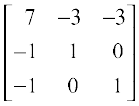
Now A (adj A) = 
= 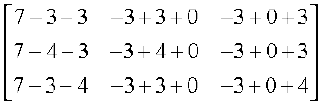
=  = (1)
= (1)  =
=  . I
. I
Also A–1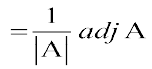 =
=  =
= 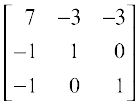
Example 25 If A = 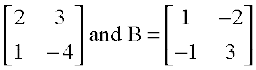 , then verify that (AB)–1 = B–1A–1.
, then verify that (AB)–1 = B–1A–1.
Solution We have AB = 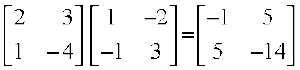
Since,  = –11 ≠ 0, (AB)–1 exists and is given by
= –11 ≠ 0, (AB)–1 exists and is given by
(AB)–1 = 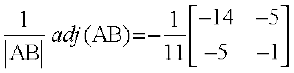
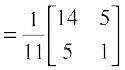
Further,  = –11 ≠ 0 and
= –11 ≠ 0 and 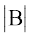 = 1 ≠ 0. Therefore, A–1 and B–1 both exist and are given by
= 1 ≠ 0. Therefore, A–1 and B–1 both exist and are given by
A–1 = 
Therefore 

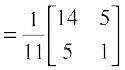
Hence (AB)–1 = B–1 A–1
Example 26 Show that the matrix A =  satisfies the equation A2 – 4A + I = O, where I is 2 × 2 identity matrix and O is 2 × 2 zero matrix. Using this equation, find A–1.
satisfies the equation A2 – 4A + I = O, where I is 2 × 2 identity matrix and O is 2 × 2 zero matrix. Using this equation, find A–1.
Solution We have 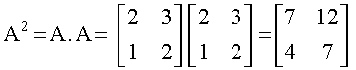
Hence 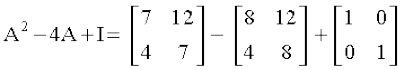
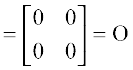
Now A2 – 4A + I = O
Therefore A A – 4A = – I
or A A (A–1) – 4 A A–1 = – I A–1 (Post multiplying by A–1 because |A| ≠ 0)
or A (A A–1) – 4I = – A–1
or AI – 4I = – A–1
or A–1 = 4I – A = 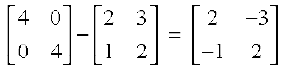
Hence 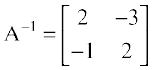
Exercise 4.5
Find adjoint of each of the matrices in Exercises 1 and 2.
1. 
2. 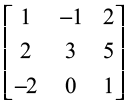
Verify A (adj A) = (adj A) A = |A| I in Exercises 3 and 4
3. 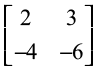
4. 
Find the inverse of each of the matrices (if it exists) given in Exercises 5 to 11.
5. 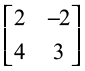
6. 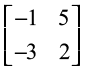
7. 
8. 
9. 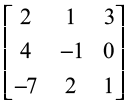
10. 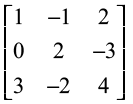
11. 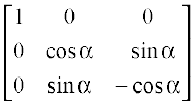
12. Let A =  and B =
and B =  . Verify that (AB)–1 = B–1 A–1.
. Verify that (AB)–1 = B–1 A–1.
13. If A =  , show that A2 – 5A + 7I = O. Hence find A–1.
, show that A2 – 5A + 7I = O. Hence find A–1.
14. For the matrix A =  , find the numbers a and b such that A2 + aA + bI = O.
, find the numbers a and b such that A2 + aA + bI = O.
15. For the matrix A = 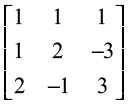
Show that A3– 6A2 + 5A + 11 I = O. Hence, find A–1.
16. If A = 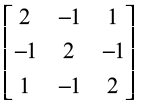
Verify that A3 – 6A2 + 9A – 4I = O and hence find A–1
17. Let A be a nonsingular square matrix of order 3 × 3. Then |adj A| is equal to
(A) |A| (B) |A|2 (C) |A|3 (D) 3|A|
18. If A is an invertible matrix of order 2, then det (A–1) is equal to
(A) det (A) (B) 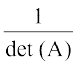 (C) 1 (D) 0
(C) 1 (D) 0
4.7 Applications of Determinants and Matrices
In this section, we shall discuss application of determinants and matrices for solving the system of linear equations in two or three variables and for checking the consistency of the system of linear equations.
Consistent system A system of equations is said to be consistent if its solution (one or more) exists.
Inconsistent system A system of equations is said to be inconsistent if its solution does not exist.
Note In this chapter, we restrict ourselves to the system of linear equations having unique solutions only.
4.7.1 Solution of system of linear equations using inverse of a matrix
Let us express the system of linear equations as matrix equations and solve them using inverse of the coefficient matrix.
Consider the system of equations
a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3
Let A = 
Then, the system of equations can be written as, AX = B, i.e.,
 =
= 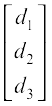
Case I If A is a nonsingular matrix, then its inverse exists. Now
AX = B
or A–1 (AX) = A–1 B (premultiplying by A–1)
or (A–1A) X = A–1 B (by associative property)
or I X = A–1 B
or X = A–1 B
This matrix equation provides unique solution for the given system of equations as inverse of a matrix is unique. This method of solving system of equations is known as Matrix Method.
Case II If A is a singular matrix, then |A| = 0.
In this case, we calculate (adj A) B.
If (adj A) B ≠ O, (O being zero matrix), then solution does not exist and the system of equations is called inconsistent.
If (adj A) B = O, then system may be either consistent or inconsistent according as the system have either infinitely many solutions or no solution.
Example 27 Solve the system of equations
2x + 5y = 1
3x + 2y = 7
Solution The system of equations can be written in the form AX = B, where
A = 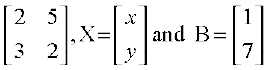
Now,  = –11 ≠ 0, Hence, A is nonsingular matrix and so has a unique solution.
= –11 ≠ 0, Hence, A is nonsingular matrix and so has a unique solution.
Note that A–1 = 
Therefore X = A–1B = – 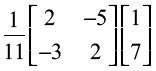
i.e. 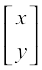 =
= 
Hence x = 3, y = – 1
Example 28 Solve the following system of equations by matrix method.
3x – 2y + 3z = 8
2x + y – z = 1
4x – 3y + 2z = 4
Solution The system of equations can be written in the form AX = B, where
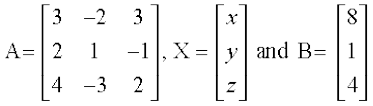
We see that
 = 3 (2 – 3) + 2(4 + 4) + 3 (– 6 – 4) = – 17 ≠ 0
= 3 (2 – 3) + 2(4 + 4) + 3 (– 6 – 4) = – 17 ≠ 0
Hence, A is nonsingular and so its inverse exists. Now
A11 = –1, A12 = – 8, A13 = –10
A21 = –5, A22 = – 6, A23 = 1
A31 = –1, A32 = 9, A33 = 7
Therefore A–1 = 
So X = 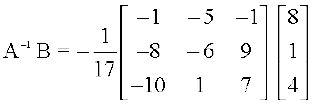
i.e. 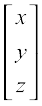 =
= 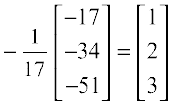
Hence x = 1, y = 2 and z = 3.
Example 29 The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.
Solution Let first, second and third numbers be denoted by x, y and z, respectively. Then, according to given conditions, we have
x + y + z = 6
y + 3z = 11
x + z = 2y or x – 2y + z = 0
This system can be written as A X = B, where
A =  , X =
, X =  and B =
and B = 
Here 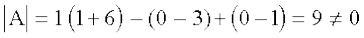 . Now we find adj A
. Now we find adj A
A11 = 1 (1 + 6) = 7, A12 = – (0 – 3) = 3, A13 = – 1
A21 = – (1 + 2) = – 3, A22 = 0, A23 = – (– 2 – 1) = 3
A31 = (3 – 1) = 2, A32 = – (3 – 0) = – 3, A33 = (1 – 0) = 1
Hence adj A = 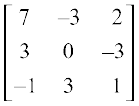
Thus A –1 =  adj (A) =
adj (A) = 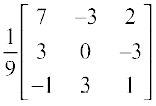
Since X = A–1 B
X = 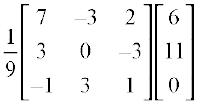
or  =
= 
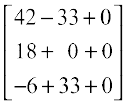 =
= 
 =
= 
Thus x = 1, y = 2, z = 3
Exercise 4.6
Examine the consistency of the system of equations in Exercises 1 to 6.
1. x + 2y = 2
2x + 3y = 3
2. 2x – y = 5
x + y = 4
3. x + 3y = 5
2x + 6y = 8
4. x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
5. 3x–y – 2z = 2
2y – z = –1
3x – 5y = 3
6. 5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = –1
Solve system of linear equations, using matrix method, in Exercises 7 to 14.
7. 5x + 2y = 4
7x + 3y = 5
8. 2x – y = –2
3x + 4y = 3
9. 4x – 3y = 3
3x – 5y = 7
10. 5x + 2y = 3
3x + 2y = 5
11. 2x + y + z = 1
x – 2y – z = 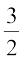
12. x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
3x – y – 2z = 3
13. 2x + 3y +3 z = 5
x – 2y + z = – 4
14. x – y + 2z = 7
3x + 4y – 5z = – 5
2x – y + 3z = 12
15. If A = 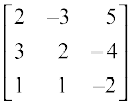 , find A–1. Using A–1 solve the system of equations
, find A–1. Using A–1 solve the system of equations
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = – 3
16. The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ` 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is ` 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is ` 70. Find cost of each item per kg by matrix method.
Miscellaneous Examples
Example 30 If a, b, c are positive and unequal, show that value of the determinant
∆ =  is negative.
is negative.
Solution Applying C1 → C1 + C2 + C3 to the given determinant, we get
∆ = 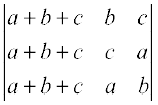 = (a + b + c)
= (a + b + c) 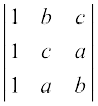
= (a + b + c) 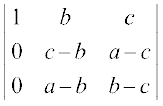 (ApplyingR2→R2–R1,andR3→R3–R1)
(ApplyingR2→R2–R1,andR3→R3–R1)
= (a + b + c) [(c – b) (b – c) – (a – c) (a – b)] (Expanding along C1)
= (a + b + c)(– a2 – b2 – c2 + ab + bc + ca)
= 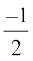 (a + b + c) (2a2 + 2b2 + 2c2 – 2ab – 2bc – 2ca)
(a + b + c) (2a2 + 2b2 + 2c2 – 2ab – 2bc – 2ca)
= 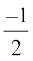 (a + b + c) [(a – b)2 + (b – c)2 + (c – a)2]
(a + b + c) [(a – b)2 + (b – c)2 + (c – a)2]
which is negative (since a + b + c > 0 and (a – b)2 + (b – c)2 + (c – a)2 > 0)
Example 31 If a, b, c, are in A.P, find value of
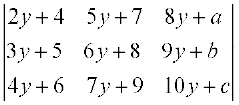
Solution Applying R1 → R1 + R3 – 2R2 to the given determinant, we obtain
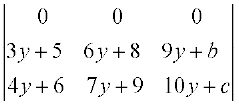 = 0 (Since 2b = a + c)
= 0 (Since 2b = a + c)
Example 32 Show that
∆ = 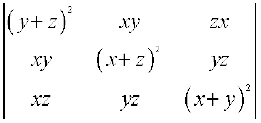 = 2xyz (x + y + z)3
= 2xyz (x + y + z)3
Solution Applying R1 → xR1, R2 → yR2 , R3 → zR3 to ∆ and dividing by xyz, we get
∆ = 
Taking common factors x, y, z from C1 C2 and C3, respectively, we get
∆ = 
Applying C2 → C2– C1, C3 → C3– C1, we have
∆ = 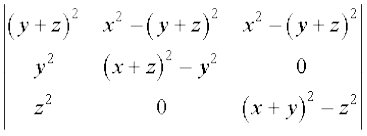
Taking common factor (x + y + z) from C2 and C3, we have
∆ = (x + y + z)2 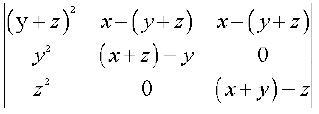
Applying R1 → R1 – (R2 + R3), we have
∆ = (x + y + z)2 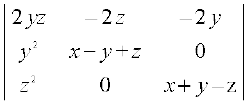
Applying C2 → (C2 + 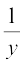 C1) and
C1) and 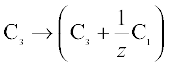 , we get
, we get
∆ = (x + y + z)2 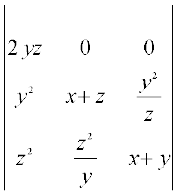
Finally expanding along R1, we have
∆ = (x + y + z)2 (2yz) [(x + z) (x + y) – yz] = (x + y + z)2 (2yz) (x2 + xy + xz)
= (x + y + z)3 (2xyz)
Example 33 Use product  to solve the system of equations
to solve the system of equations
x – y + 2z = 1
2y – 3z = 1
3x – 2y + 4z = 2
Solution Consider the product 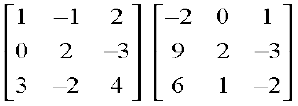
= 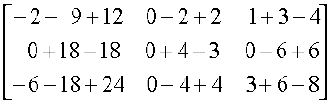 =
= 
Hence 
Now, given system of equations can be written, in matrix form, as follows
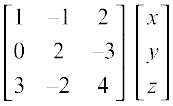 =
= 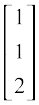
or  =
= 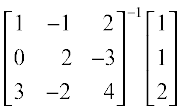 =
= 
= 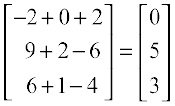
Hence x = 0, y = 5 and z = 3
Example 34 Prove that
∆ = 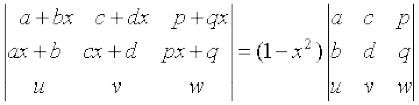
Solution Applying R1 → R1 – x R2 to ∆, we get
∆ = 
= 
Applying R2 → R2 – x R1, we get
∆ = 
Miscellaneous Exercises on Chapter 4
1. Prove that the determinant 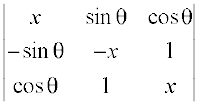 is independent of θ.
is independent of θ.
2. Without expanding the determinant, prove that 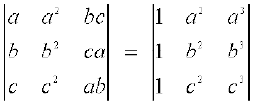 .
.
3. Evaluate 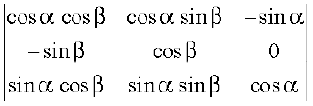 .
.
4. If a, b and c are real numbers, and
∆ = 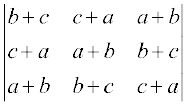 = 0,
= 0,
Show that either a + b + c = 0 or a = b = c.
5. Solve the equation 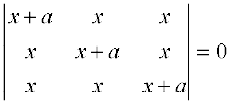 , a ≠ 0
, a ≠ 0
6. Prove that 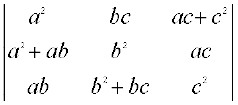 = 4a2b2c2
= 4a2b2c2
7. If A–1 = 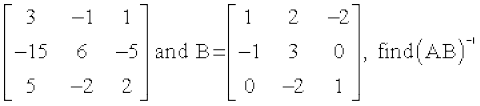
8. Let A = 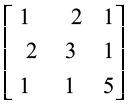 . Verify that
. Verify that
(i) [adj A]–1 = adj (A–1) (ii) (A–1)–1 = A
9. Evaluate 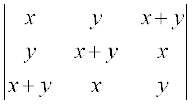
10. Evaluate 
Using properties of determinants in Exercises 11 to 15, prove that:
11. 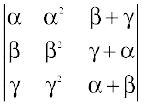 = (β – γ) (γ – α) (α – β) (α + β + γ)
= (β – γ) (γ – α) (α – β) (α + β + γ)
12. 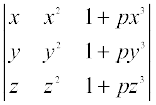 = (1 + pxyz) (x – y) (y – z) (z – x), where p is any scalar.
= (1 + pxyz) (x – y) (y – z) (z – x), where p is any scalar.
13. 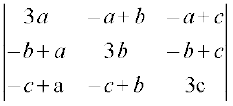 = 3(a + b + c) (ab + bc + ca)
= 3(a + b + c) (ab + bc + ca)
14. 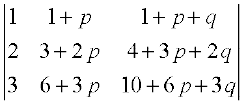 = 1
= 1
15. 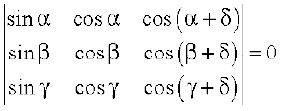
16. Solve the system of equations
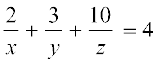
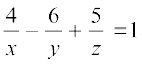
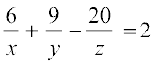
Choose the correct answer in Exercise 17 to 19.
17. If a, b, c, are in A.P, then the determinant
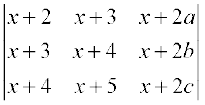 is
is
(A) 0 (B) 1 (C) x (D) 2x
18. If x, y, z are nonzero real numbers, then the inverse of matrix 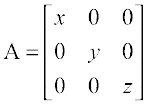 is
is
(A) 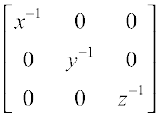 (B)
(B) 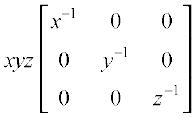
(C) 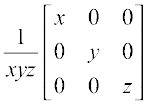 (D)
(D) 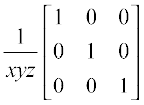
19. Let A = 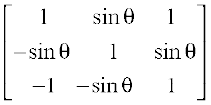 , where 0 ≤ θ ≤ 2π. Then
, where 0 ≤ θ ≤ 2π. Then
(A) Det(A) = 0 (B) Det(A) ∈ (2, ∞)
(C) Det(A) ∈ (2, 4) (D) Det(A) ∈ [2, 4]
Summary
 Determinant of a matrix A = [a11]1×1 is given by |a11| = a11
Determinant of a matrix A = [a11]1×1 is given by |a11| = a11
 Determinant of a matrix
Determinant of a matrix  is given by
is given by
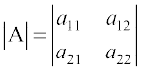 = a11 a22 – a12 a21
= a11 a22 – a12 a21
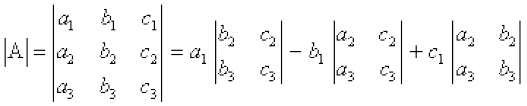
 Determinant of a matrix
Determinant of a matrix  is given by (expanding along R1)
is given by (expanding along R1)
For any square matrix A, the |A| satisfy following properties.
 |A′| = |A|, where A′ = transpose of A.
|A′| = |A|, where A′ = transpose of A.
 If we interchange any two rows (or columns), then sign of determinant changes.
If we interchange any two rows (or columns), then sign of determinant changes.
 If any two rows or any two columns are identical or proportional, then value of determinant is zero.
If any two rows or any two columns are identical or proportional, then value of determinant is zero.
 If we multiply each element of a row or a column of a determinant by constant k, then value of determinant is multiplied by k.
If we multiply each element of a row or a column of a determinant by constant k, then value of determinant is multiplied by k.
 Multiplying a determinant by k means multiply elements of only one row
Multiplying a determinant by k means multiply elements of only one row
(or one column) by k.
 If
If 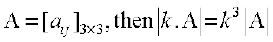
 If elements of a row or a column in a determinant can be expressed as sum of two or more elements, then the given determinant can be expressed as sum of two or more determinants.
If elements of a row or a column in a determinant can be expressed as sum of two or more elements, then the given determinant can be expressed as sum of two or more determinants.
 If to each element of a row or a column of a determinant the equimultiples of corresponding elements of other rows or columns are added, then value of determinant remains same.
If to each element of a row or a column of a determinant the equimultiples of corresponding elements of other rows or columns are added, then value of determinant remains same.
 Area of a triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is given by
Area of a triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is given by
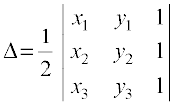
 Minor of an element aij of the determinant of matrix A is the determinant obtained by deleting ith row and jth column and denoted by Mij.
Minor of an element aij of the determinant of matrix A is the determinant obtained by deleting ith row and jth column and denoted by Mij.
 Cofactor of aij of given by Aij = (– 1)i+j Mij
Cofactor of aij of given by Aij = (– 1)i+j Mij
 Value of determinant of a matrix A is obtained by sum of product of elements of a row (or a column) with corresponding cofactors. For example,
Value of determinant of a matrix A is obtained by sum of product of elements of a row (or a column) with corresponding cofactors. For example,
 = a11 A11 + a12 A12 + a13 A13.
= a11 A11 + a12 A12 + a13 A13.
 If elements of one row (or column) are multiplied with cofactors of elements of any other row (or column), then their sum is zero. For example, a11 A21 + a12 A22 + a13 A23 = 0
If elements of one row (or column) are multiplied with cofactors of elements of any other row (or column), then their sum is zero. For example, a11 A21 + a12 A22 + a13 A23 = 0
 If
If 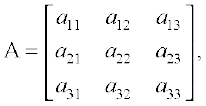 then
then 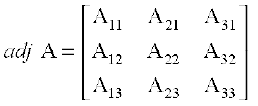 , where Aij is cofactor of aij
, where Aij is cofactor of aij
 A (adj A) = (adj A) A = |A| I, where A is square matrix of order n.
A (adj A) = (adj A) A = |A| I, where A is square matrix of order n.
 A square matrix A is said to be singular or non-singular according as
A square matrix A is said to be singular or non-singular according as
|A| = 0 or |A| ≠ 0.
 If AB = BA = I, where B is square matrix, then B is called inverse of A.
If AB = BA = I, where B is square matrix, then B is called inverse of A.
Also A–1 = B or B–1 = A and hence (A–1)–1 = A.
 A square matrix A has inverse if and only if A is non-singular.
A square matrix A has inverse if and only if A is non-singular.

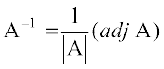
 If a1 x + b1 y + c1 z = d1
If a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3,
then these equations can be written as A X = B, where
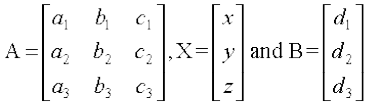
 Unique solution of equation AX = B is given by X = A–1 B, where
Unique solution of equation AX = B is given by X = A–1 B, where  .
.
 A system of equation is consistent or inconsistent according as its solution exists or not.
A system of equation is consistent or inconsistent according as its solution exists or not.
 For a square matrix A in matrix equation AX = B
For a square matrix A in matrix equation AX = B
(i) |A| ≠ 0, there exists unique solution
(ii) |A| = 0 and (adj A) B ≠ 0, then there exists no solution
(iii) |A| = 0 and (adj A) B = 0, then system may or may not be consistent.
Historical Note
The Chinese method of representing the coefficients of the unknowns of several linear equations by using rods on a calculating board naturally led to the discovery of simple method of elimination. The arrangement of rods was precisely that of the numbers in a determinant. The Chinese, therefore, early developed the idea of subtracting columns and rows as in simplification of a determinant
Mikami, China, pp 30, 93.
Seki Kowa, the greatest of the Japanese Mathematicians of seventeenth century in his work ‘Kai Fukudai no Ho’ in 1683 showed that he had the idea of determinants and of their expansion. But he used this device only in eliminating a quantity from two equations and not directly in the solution of a set of simultaneous linear equations. T. Hayashi, “The Fakudoi and Determinants in Japanese Mathematics,” in the proc. of the Tokyo Math. Soc., V.
Vendermonde was the first to recognise determinants as independent functions. He may be called the formal founder. Laplace (1772), gave general method of expanding a determinant in terms of its complementary minors. In 1773 Lagrange treated determinants of the second and third orders and used them for purpose other than the solution of equations. In 1801, Gauss used determinants in his theory of numbers.
The next great contributor was Jacques - Philippe - Marie Binet, (1812) who stated the theorem relating to the product of two matrices of m-columns and n-rows, which for the special case of m = n reduces to the multiplication theorem.
Also on the same day, Cauchy (1812) presented one on the same subject. He used the word ‘determinant’ in its present sense. He gave the proof of multiplication theorem more satisfactory than Binet’s.
The greatest contributor to the theory was Carl Gustav Jacob Jacobi, after this the word determinant received its final acceptance.
