Solution of Chapter 4. Determinants (Mathemetics Part-I Book)
Chapter Exercises
Exercise 4.1
Exercise 4.2
Exercise 4.3
Exercise 4.4
Exercise 4.5
Exercise 4.6
Miscellaneous Exercise
3
Evaluate 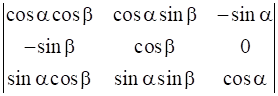
9
Evaluate 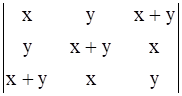
10
Evaluate 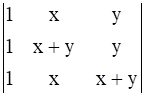
11
Prove that 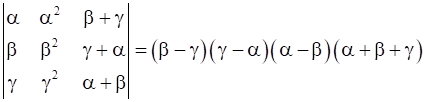
13
Prove that 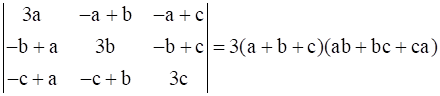
14
Prove that 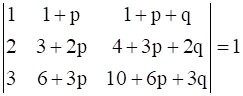
15
Prove that 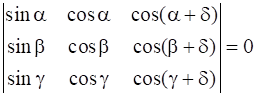
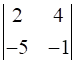
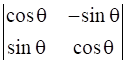
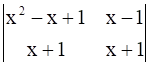
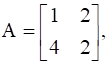
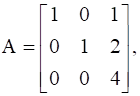
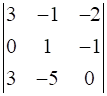
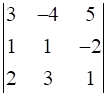
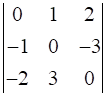
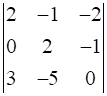
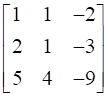
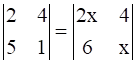
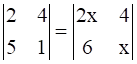
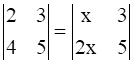
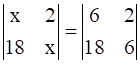
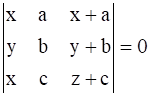
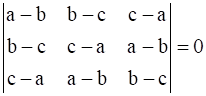
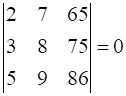
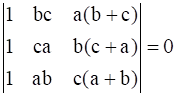
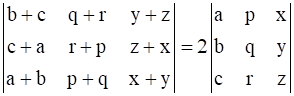
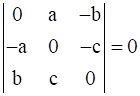
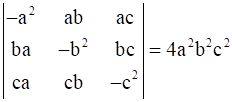
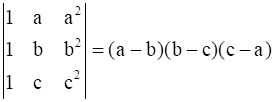
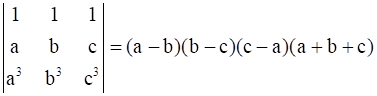
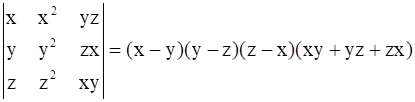
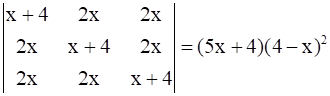
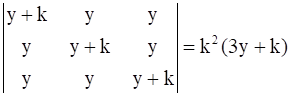
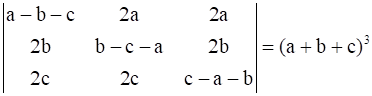
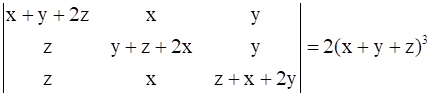
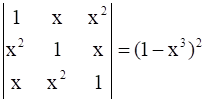
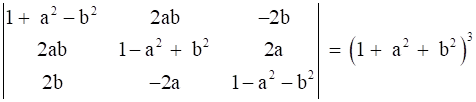
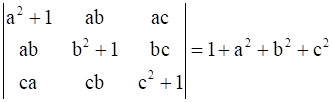
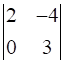
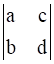
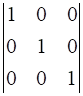
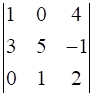
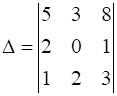
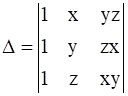 .
.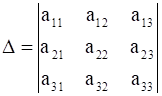
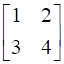
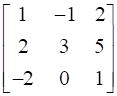
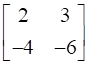
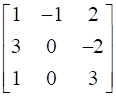
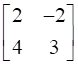
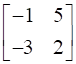
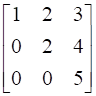
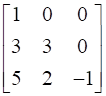
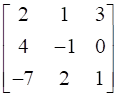
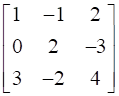
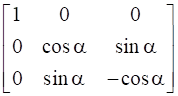
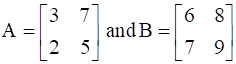
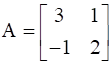
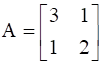
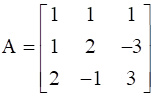
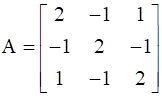
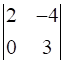
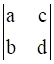
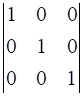
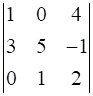
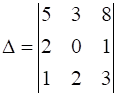
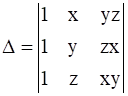
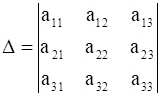
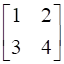
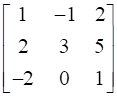
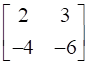
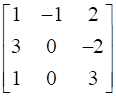
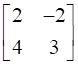
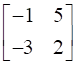
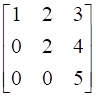
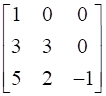
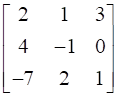
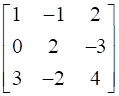
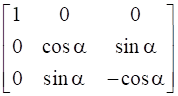
![a = [ ll 3&7 2&5 ] b = [ ll 6&8 7&9 ]](https://static.insightsonindia.in/ncertusercontent/solutions/?domain=gF&l=PROJ28781/1554209794065194.png)
![a = [ cc 3&1 -1&2 ]](https://static.insightsonindia.in/ncertusercontent/solutions/?domain=gF&l=PROJ28781/1554209799326247.png)
![a = [ ll 3&1 1&2 ]](https://static.insightsonindia.in/ncertusercontent/solutions/?domain=gF&l=PROJ28781/1554209802337249.png)
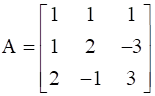
![a = [ ccc 2&-1&1 -1&2&-1 1&-1&2 ]](https://static.insightsonindia.in/ncertusercontent/solutions/?domain=gF&l=PROJ28781/1554209812139147.png)
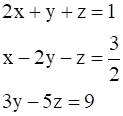
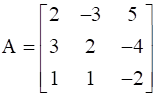
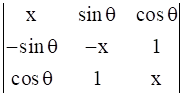
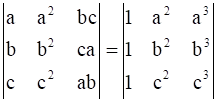
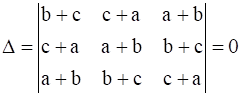
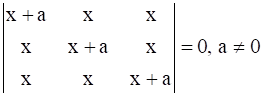
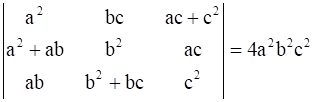
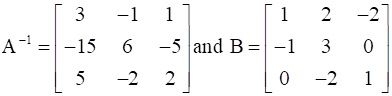
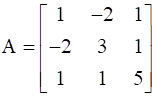
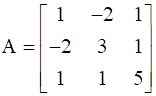
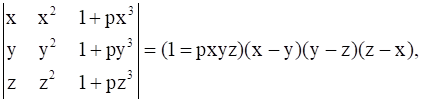
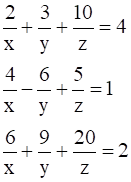
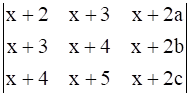 is
is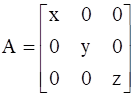 is
is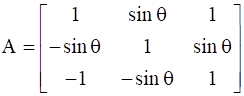 , where 0 ≤ θ ≤ 2π. Then
, where 0 ≤ θ ≤ 2π. Then