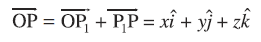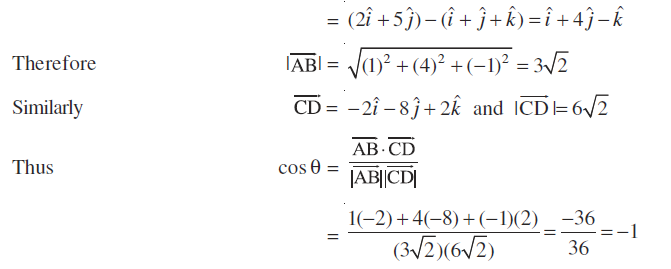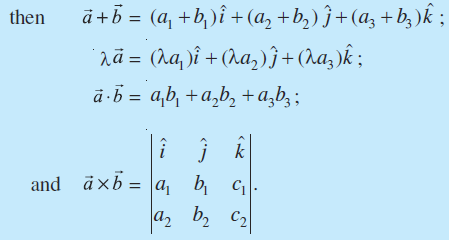Table of Contents
Chapter 10
Vector Algebra
☘ In most sciences one generation tears down what another has built and what one has established another undoes. In Mathematics alone each generation builds a new story to the old structure. – Herman Hankel ☘
10.1 Introduction
In our day to day life, we come across many queries such as – What is your height? How should a football player hit the ball to give a pass to another player of his team? Observe that a possible answer to the first query may be 1.6 meters, a quantity that involves only one value (magnitude) which is a real number. Such quantities are called scalars. However, an answer to the second query is a quantity (called force) which involves muscular strength (magnitude) and direction (in which another player is positioned). Such quantities are called vectors. In mathematics, physics and engineering, we frequently come across with both types of quantities, namely, scalar quantities such as length, mass, time, distance, speed, area, volume, temperature, work, money, voltage, density, resistance etc. and vector quantities like displacement, velocity, acceleration, force, weight, momentum, electric field intensity etc.

In this chapter, we will study some of the basic concepts about vectors, various operations on vectors, and their algebraic and geometric properties. These two type of properties, when considered together give a full realisation to the concept of vectors, and lead to their vital applicability in various areas as mentioned above.
10.2 Some Basic Concepts
Let ‘l’ be any straight line in plane or three dimensional space. This line can be given two directions by means of arrowheads. A line with one of these directions prescribed is called a directed line (Fig 10.1 (i), (ii)).
Now observe that if we restrict the line l to the line segment AB, then a magnitude is prescribed on the line l with one of the two directions, so that we obtain a directed line segment (Fig 10.1(iii)). Thus, a directed line segment has magnitude as well as direction.
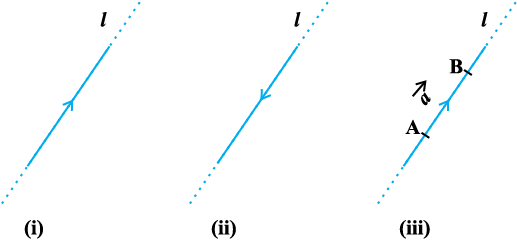
Fig 10.1
1 A quantity that has magnitude as well as direction is called a vector.
Notice that a directed line segment is a vector (Fig 10.1(iii)), denoted as  or simply as
or simply as 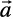 , and read as ‘vector
, and read as ‘vector 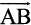 ’ or ‘vector
’ or ‘vector 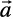 ’.
’.
The point A from where the vector 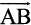 starts is called its initial point, and the point B where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as |
starts is called its initial point, and the point B where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as |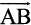 |, or |
|, or |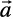 |, or a. The arrow indicates the direction of the vector.
|, or a. The arrow indicates the direction of the vector.
☘ Note Since the length is never negative, the notation |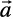 | < 0 has no meaning.
| < 0 has no meaning.
Position Vector
From Class XI, recall the three dimensional right handed rectangular coordinate system (Fig 10.2(i)). Consider a point P in space, having coordinates (x, y, z) with respect to the origin O(0, 0, 0). Then, the vector 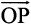 having O and P as its initial and terminal points, respectively, is called the position vector of the point P with respect
having O and P as its initial and terminal points, respectively, is called the position vector of the point P with respect
to O. Using distance formula (from Class XI), the magnitude of 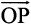 (or
(or 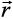 ) is given by
) is given by
|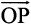 |=
|= 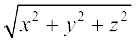
In practice, the position vectors of points A, B, C, etc., with respect to the origin O are denoted by 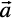 ,
,  ,
,  , etc., respectively (Fig 10.2 (ii)).
, etc., respectively (Fig 10.2 (ii)).
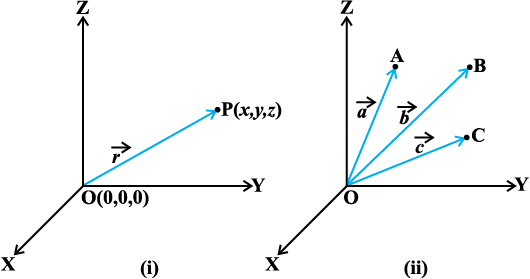
Fig 10.2
Direction Cosines
Consider the position vector  of a point P(x, y, z) as in Fig 10.3. The angles α, β, γ made by the vector
of a point P(x, y, z) as in Fig 10.3. The angles α, β, γ made by the vector  with the positive directions of x, y and z-axes respectively, are called its direction angles. The cosine values of these angles, i.e., cosα, cosβ and cosγ are called direction cosines of the vector
with the positive directions of x, y and z-axes respectively, are called its direction angles. The cosine values of these angles, i.e., cosα, cosβ and cosγ are called direction cosines of the vector  , and usually denoted by l, m and n, respectively.
, and usually denoted by l, m and n, respectively.
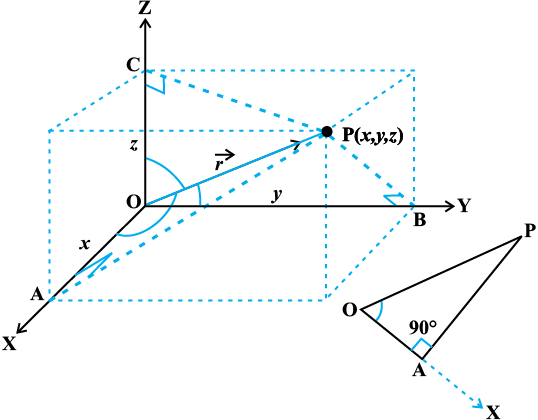
Fig 10.3
From Fig 10.3, one may note that the triangle OAP is right angled, and in it, we have 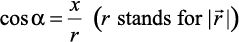 . Similarly, from the right angled triangles OBP and OCP, we may write
. Similarly, from the right angled triangles OBP and OCP, we may write 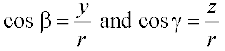 . Thus, the coordinates of the point P may also be expressed as (lr, mr,nr). The numbers lr, mr and nr, proportional to the direction cosines are called as direction ratios of vector
. Thus, the coordinates of the point P may also be expressed as (lr, mr,nr). The numbers lr, mr and nr, proportional to the direction cosines are called as direction ratios of vector 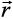 , and denoted as a, b and c, respectively.
, and denoted as a, b and c, respectively.
☘ Note One may note that l2 + m2 + n2 = 1 but a2 + b2 + c2 ≠ 1, in general.
10.3 Types of Vectors
Zero Vector A vector whose initial and terminal points coincide, is called a zero vector (or null vector), and denoted as  . Zero vector can not be assigned a definite direction as it has zero magnitude. Or, alternatively otherwise, it may be regarded as having any direction. The vectors
. Zero vector can not be assigned a definite direction as it has zero magnitude. Or, alternatively otherwise, it may be regarded as having any direction. The vectors  represent the zero vector,
represent the zero vector,
Unit Vector A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector. The unit vector in the direction of a given vector 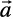 is denoted by
is denoted by 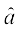 .
.
Coinitial Vectors Two or more vectors having the same initial point are called coinitial vectors.
Collinear Vectors Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.
Equal Vectors Two vectors 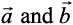 are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written
are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written
as 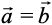 .
.
Negative of a Vector A vector whose magnitude is the same as that of a given vector (say, 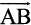 ), but direction is opposite to that of it, is called negative of the given vector. For example, vector
), but direction is opposite to that of it, is called negative of the given vector. For example, vector 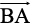 is negative of the vector
is negative of the vector 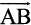 , and written as
, and written as 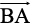 = –
= – 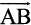 .
.
Remark The vectors defined above are such that any of them may be subject to its parallel displacement without changing its magnitude and direction. Such vectors are called free vectors. Throughout this chapter, we will be dealing with free vectors only.
Example 1 Represent graphically a displacement of 40 km, 30° west of south.
Solution The vector 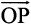 represents the required displacement (Fig 10.4).
represents the required displacement (Fig 10.4).
Fig 10.4
Example 2 Classify the following measures as scalars and vectors.
(i) 5 seconds
(ii) 1000 cm3
(iii) 10 Newton (iv) 30 km/hr (v) 10 g/cm3
(vi) 20 m/s towards north
Solution
(i) Time-scalar
(ii) Volume-scalar
(iii) Force-vector
(iv) Speed-scalar
(v) Density-scalar
(vi) Velocity-vector
Example 3 In Fig 10.5, which of the vectors are:
Solution
(i) Collinear .
.
(ii) Equal  .
.
(iii) Coinitial  .
.
Fig 10.5
Exercise 10.1
1. Represent graphically a displacement of 40 km, 30° east of north.
2. Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 watt
(v) 10–19 coulomb
(vi) 20 m/s2
3. Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
4. In Fig 10.6 (a square), identify the following vectors.
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal

Fig 10.6
5. Answer the following as true or false.
(i)  and –
and – 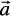 are collinear.
are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
10.4 Addition of Vectors
A vector 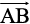 simply means the displacement from a point A to the point B. Now consider a situation that a girl moves from A to B and then from B to C
simply means the displacement from a point A to the point B. Now consider a situation that a girl moves from A to B and then from B to C
(Fig 10.7). The net displacement made by the girl from point A to the point C, is given by the vector 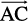 and expressed as
and expressed as
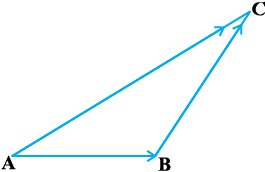
Fig 10.7
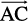 =
= 
This is known as the triangle law of vector addition.
In general, if we have two vectors 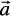 and
and  (Fig 10.8 (i)), then to add them, they are positioned so that the initial point of one coincides with the terminal point of the other (Fig 10.8(ii)).
(Fig 10.8 (i)), then to add them, they are positioned so that the initial point of one coincides with the terminal point of the other (Fig 10.8(ii)).
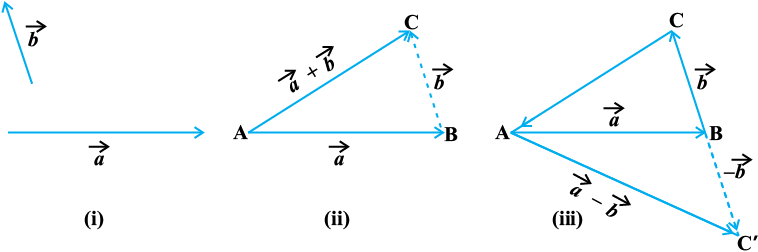
Fig 10.8
For example, in Fig 10.8 (ii), we have shifted vector 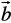 without changing its magnitude and direction, so that it’s initial point coincides with the terminal point of
without changing its magnitude and direction, so that it’s initial point coincides with the terminal point of 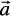 . Then, the vector
. Then, the vector 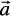 +
+ 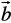 , represented by the third side AC of the triangle ABC, gives us the sum (or resultant) of the vectors
, represented by the third side AC of the triangle ABC, gives us the sum (or resultant) of the vectors 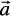 and
and 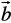 i.e., in triangle ABC (Fig 10.8 (ii)), we have
i.e., in triangle ABC (Fig 10.8 (ii)), we have
 =
= 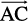
Now again, since 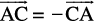 , from the above equation, we have
, from the above equation, we have
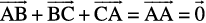
This means that when the sides of a triangle are taken in order, it leads to zero resultant as the initial and terminal points get coincided (Fig 10.8(iii)).
Now, construct a vector  so that its magnitude is same as the vector
so that its magnitude is same as the vector 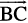 , but the direction opposite to that of it (Fig 10.8 (iii)), i.e.,
, but the direction opposite to that of it (Fig 10.8 (iii)), i.e.,
 =
= 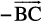
Then, on applying triangle law from the Fig 10.8 (iii), we have
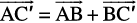 =
= 
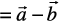
The vector 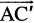 is said to represent the difference of
is said to represent the difference of  .
.
Now, consider a boat in a river going from one bank of the river to the other in a direction perpendicular to the flow of the river. Then, it is acted upon by two velocity vectors–one is the velocity imparted to the boat by its engine and other one is the velocity of the flow of river water. Under the simultaneous influence of these two velocities, the boat in actual starts travelling with a different velocity. To have a precise idea about the effective speed and direction (i.e., the resultant velocity) of the boat, we have the following law of vector addition.
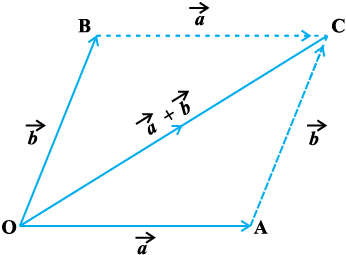
Fig 10.9
If we have two vectors  represented by the two adjacent sides of a parallelogram in magnitude and direction (Fig 10.9), then their sum
represented by the two adjacent sides of a parallelogram in magnitude and direction (Fig 10.9), then their sum  is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is known as the parallelogram law of vector addition.
is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is known as the parallelogram law of vector addition.
Note From Fig 10.9, using the triangle law, one may note that
 =
= 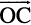
or 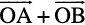 =
= 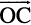 (since
(since 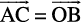 )
)
which is parallelogram law. Thus, we may say that the two laws of vector addition are equivalent to each other.
Properties of vector addition
Property 1 For any two vectors  ,
,
 =
= 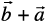 (Commutative property)
(Commutative property)
Proof Consider the parallelogram ABCD
(Fig 10.10). Let  then using the triangle law, from triangle ABC, we have
then using the triangle law, from triangle ABC, we have

Now, since the opposite sides of a parallelogram are equal and parallel, from
Fig10.10, we have, 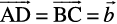 and
and 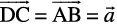 . Again using triangle law, from triangle ADC, we have
. Again using triangle law, from triangle ADC, we have
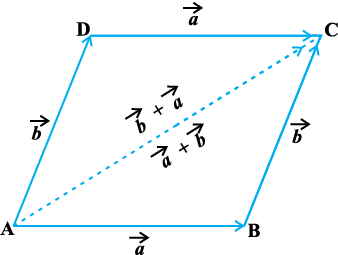
Fig 10.10
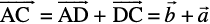
Hence 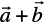 =
= 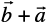
Property 2 For any three vectors 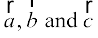
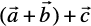 =
= 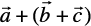 (Associative property)
(Associative property)
Proof Let the vectors  be represented by
be represented by 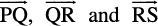 , respectively, as shown in Fig 10.11(i) and (ii).
, respectively, as shown in Fig 10.11(i) and (ii).
 Fig 10.11
Fig 10.11
Then 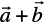 =
= 
and 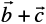 =
= 
So  =
= 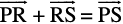
and 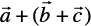 =
= 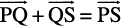
Hence 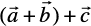 =
= 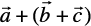
Remark The associative property of vector addition enables us to write the sum of three vectors 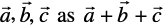 without using brackets.
without using brackets.
Note that for any vector 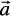 , we have
, we have
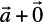 =
= 
Here, the zero vector 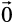 is called the additive identity for the vector addition.
is called the additive identity for the vector addition.
10.5 Multiplication of a Vector by a Scalar
Let  be a given vector and λ a scalar. Then the product of the vector
be a given vector and λ a scalar. Then the product of the vector  by the scalar λ, denoted as λ
by the scalar λ, denoted as λ , is called the multiplication of vector
, is called the multiplication of vector  by the scalar λ. Note that, λ
by the scalar λ. Note that, λ is also a vector, collinear to the vector
is also a vector, collinear to the vector  . The vector λ
. The vector λ has the direction same (or opposite) to that of vector
has the direction same (or opposite) to that of vector  according as the value of λ is positive (or negative). Also, the magnitude of vector λ
according as the value of λ is positive (or negative). Also, the magnitude of vector λ is |λ| times the magnitude of the vector
is |λ| times the magnitude of the vector  , i.e.,
, i.e.,
|λ | = |λ||
| = |λ|| |
|
A geometric visualisation of multiplication of a vector by a scalar is given in Fig 10.12.

Fig 10.12
When λ = –1, then λ = –
= –  , which is a vector having magnitude equal to the magnitude of
, which is a vector having magnitude equal to the magnitude of  and direction opposite to that of the direction of
and direction opposite to that of the direction of  . The vector –
. The vector – is called the negative (or additive inverse) of vector
is called the negative (or additive inverse) of vector  and we always have
and we always have
 + (–
+ (–  ) = (–
) = (–  ) +
) +  =
= 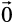
Also, if 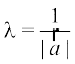 , provided
, provided  ≠ 0 i.e.
≠ 0 i.e.  is not a null vector, then
is not a null vector, then
|λ | =|λ||
| =|λ|| | =
| = 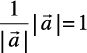
So, λ  represents the unit vector in the direction of
represents the unit vector in the direction of  . We write it as
. We write it as

☘ Note For any scalar 
10.5.1 Components of a vector
Let us take the points A(1, 0, 0), B(0, 1, 0) and C(0, 0, 1) on the x-axis, y-axis and
z-axis, respectively. Then, clearly
| |= 1, |
|= 1, | |= 1 and |
|= 1 and | |= 1
|= 1
The vectors  , each having magnitude 1, are called unit vectors along the axes OX, OY and OZ, respectively, and denoted by
, each having magnitude 1, are called unit vectors along the axes OX, OY and OZ, respectively, and denoted by 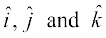 , respectively (Fig 10.13).
, respectively (Fig 10.13).
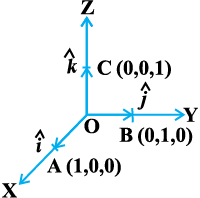
Fig 10.13
Now, consider the position vector  of a point P(x, y, z) as in Fig 10.14. Let P1 be the foot of the perpendicular from P on the plane XOY.
of a point P(x, y, z) as in Fig 10.14. Let P1 be the foot of the perpendicular from P on the plane XOY.
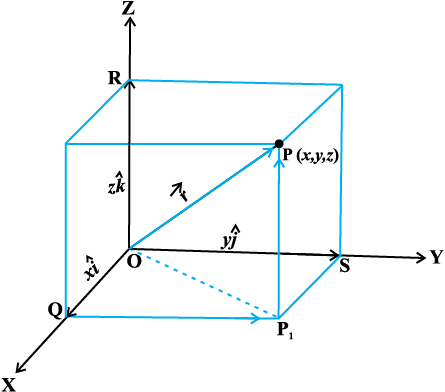
Fig 10.14
We, thus, see that P1 P is parallel to z-axis. As 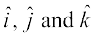 are the unit vectors along the x, y and z-axes, respectively, and by the of the coordinates of P,
are the unit vectors along the x, y and z-axes, respectively, and by the of the coordinates of P,
we have 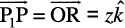 . Similarly,
. Similarly, 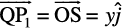 and
and 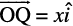 .
.
Therefore, it follows that 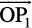 =
= 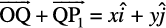
and
Hence, the position vector of P with reference to O is given by
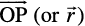 =
= 
This form of any vector is called its component form. Here, x, y and z are called as the scalar components of 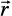 , and
, and 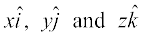 are called the vector components of
are called the vector components of 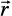 along the respective axes. Sometimes x, y and z are also termed as rectangular components.
along the respective axes. Sometimes x, y and z are also termed as rectangular components.
The length of any vector 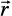 =
=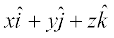 , is readily determined by applying the Pythagoras theorem twice. We note that in the right angle triangle OQP1 (Fig 10.14)
, is readily determined by applying the Pythagoras theorem twice. We note that in the right angle triangle OQP1 (Fig 10.14)
 =
= 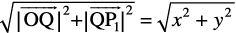 ,
,
and in the right angle triangle OP1P, we have
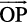 =
= 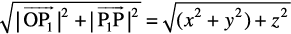
Hence, the length of any vector 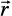 =
=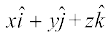 is given by
is given by
|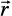 | =
| = 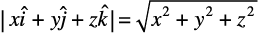
If 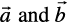 are any two vectors given in the component form
are any two vectors given in the component form 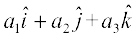 and
and 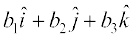 , respectively, then
, respectively, then
(i) the sum (or resultant) of the vectors 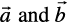 is given by
is given by
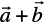 =
= 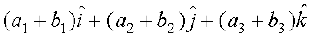
(ii) the difference of the vector  is given by
is given by
 =
= 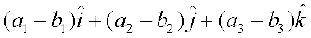
(iii) the vectors 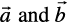 are equal if and only if
are equal if and only if
a1 = b1, a2 = b2 and a3 = b3
(iv) the multiplication of vector  by any scalar λ is given by
by any scalar λ is given by
λ =
= 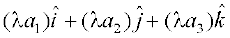
The addition of vectors and the multiplication of a vector by a scalar together give the following distributive laws:
Let 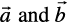 be any two vectors, and k and m be any scalars. Then
be any two vectors, and k and m be any scalars. Then
(i) 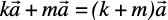
(ii) 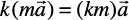
(iii) 
Remarks
(i) One may observe that whatever be the value of λ, the vector λ is always collinear to the vector
is always collinear to the vector  . In fact, two vectors
. In fact, two vectors 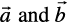 are collinear if and only if there exists a nonzero scalar λ such that
are collinear if and only if there exists a nonzero scalar λ such that 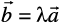 . If the vectors
. If the vectors 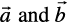 are given in the component form, i.e.
are given in the component form, i.e.  =
= 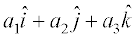 and
and 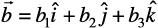 , then the two vectors are collinear if and only if
, then the two vectors are collinear if and only if
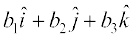 =
= 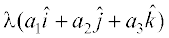
⇔ 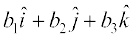 =
= 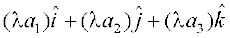
⇔ 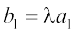 ,
, 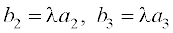
⇔ 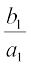 =
= 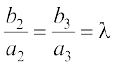
(ii) If  =
= 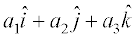 , then a1, a2, a3 are also called direction ratios of
, then a1, a2, a3 are also called direction ratios of  .
.
(iii) In case if it is given that l, m, n are direction cosines of a vector, then 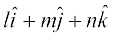 =
= 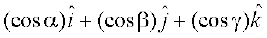 is the unit vector in the direction of that vector, where α, β and γ are the angles which the vector makes with x, y and z axes respectively.
is the unit vector in the direction of that vector, where α, β and γ are the angles which the vector makes with x, y and z axes respectively.
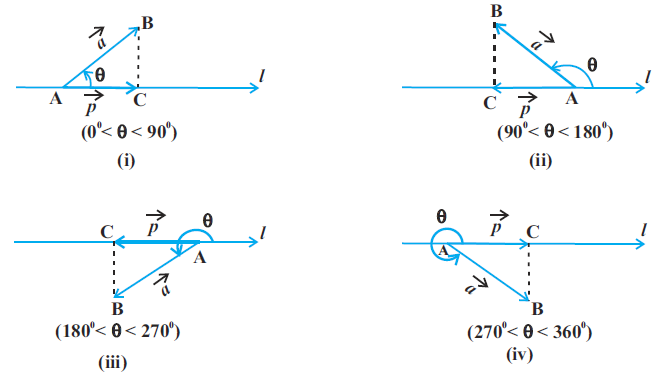
Example 4 Find the values of x, y and z so that the vectors 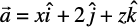 and
and  are equal.
are equal.
Solution Note that two vectors are equal if and only if their corresponding components are equal. Thus, the given vectors 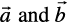 will be equal if and only if
will be equal if and only if
x = 2, y = 2, z = 1
Example 5 Let 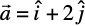 and
and 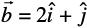 . Is
. Is 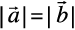 ? Are the vectors
? Are the vectors 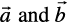 equal?
equal?
Solution We have 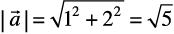 and
and 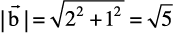
So, 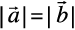 . But, the two vectors are not equal since their corresponding components are distinct.
. But, the two vectors are not equal since their corresponding components are distinct.
Example 6 Find unit vector in the direction of vector 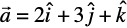
Solution The unit vector in the direction of a vector  is given by
is given by 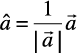 .
.
Now 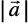 =
= 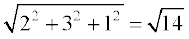
Therefore 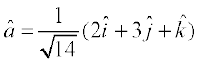 =
= 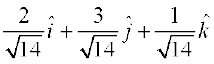
Example 7 Find a vector in the direction of vector 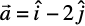 that has magnitude
that has magnitude
7 units.
Solution The unit vector in the direction of the given vector  is
is
 =
= 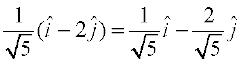
Therefore, the vector having magnitude equal to 7 and in the direction of  is
is
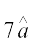 =
= 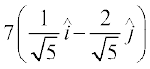 =
= 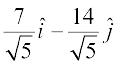
Example 8 Find the unit vector in the direction of the sum of the vectors, 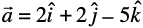 and
and  .
.
Solution The sum of the given vectors is

and 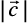 =
= 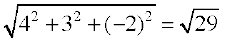
Thus, the required unit vector is

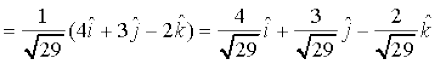
Example 9 Write the direction ratio’s of the vector  and hence calculate its direction cosines.
and hence calculate its direction cosines.
Solution Note that the direction ratio’s a, b, c of a vector  are just
are just
the respective components x, y and z of the vector. So, for the given vector, we have
a = 1, b = 1 and c = –2. Further, if l, m and n are the direction cosines of the given vector, then
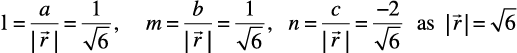
Thus, the direction cosines are 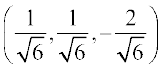 .
.
10.5.2 Vector joining two points
If P1(x1, y1, z1) and P2(x2, y2, z2) are any two points, then the vector joining P1 and P2 is the vector 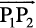 (Fig 10.15).
(Fig 10.15).
Joining the points P1 and P2 with the origin O, and applying triangle law, from the triangle OP1P2, we have
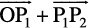 =
= 
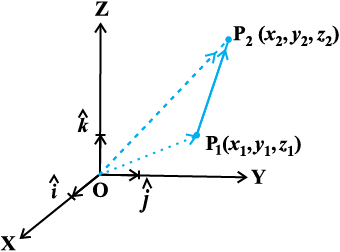
Fig 10.15
Using the properties of vector addition, the above equation becomes
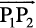 =
= 
i.e. 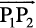 =
= 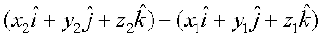
= 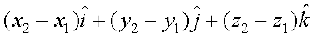
The magnitude of vector 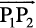 is given by
is given by
|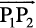 | =
| = 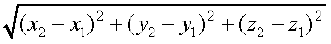
Example 10 Find the vector joining the points P(2, 3, 0) and Q(– 1, – 2, – 4) directed from P to Q.
Solution Since the vector is to be directed from P to Q, clearly P is the initial point
and Q is the terminal point. So, the required vector joining P and Q is the vector 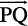 , given by
, given by
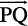 =
= 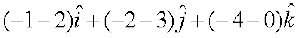
i.e. 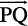 =
= 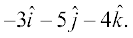
10.5.3 Section formula
Let P and Q be two points represented by the position vectors  , respectively, with respect to the origin O. Then the line segment joining the points P and Q may be divided by a third point, say R, in two ways – internally (Fig 10.16) and externally (Fig 10.17). Here, we intend to find the position vector
, respectively, with respect to the origin O. Then the line segment joining the points P and Q may be divided by a third point, say R, in two ways – internally (Fig 10.16) and externally (Fig 10.17). Here, we intend to find the position vector  for the point R with respect to the origin O. We take the two cases one by one.
for the point R with respect to the origin O. We take the two cases one by one.
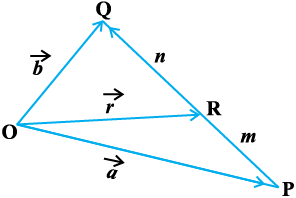
Fig 10.16
Case I When R divides PQ internally (Fig 10.16).
If R divides  such that
such that 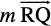 =
=  ,
,
where m and n are positive scalars, we say that the point R divides 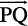 internally in the ratio of m : n. Now from triangles ORQ and OPR, we have
internally in the ratio of m : n. Now from triangles ORQ and OPR, we have
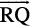 =
= 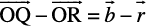
and 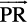 =
= 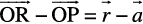 ,
,
Therefore, we have 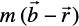 =
= 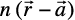 (Why?)
(Why?)
or 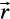 =
=  (on simplification)
(on simplification)
Hence, the position vector of the point R which divides P and Q internally in the ratio of m : n is given by
 =
= 
Case II When R divides PQ externally (Fig 10.17). We leave it to the reader as an exercise to verify that the position vector of the point R which divides the line segment PQ externally in the ratio
m : n  is given by
is given by
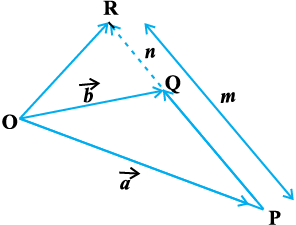
Fig 10.17
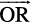 =
= 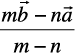
Remark If R is the midpoint of PQ , then m = n. And therefore, from Case I, the midpoint R of 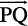 , will have its position vector as
, will have its position vector as
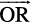 =
= 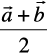
Example 11 Consider two points P and Q with position vectors 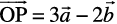 and
and 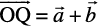 . Find the position vector of a point R which divides the line joining P and Q in the ratio 2:1, (i) internally, and (ii) externally.
. Find the position vector of a point R which divides the line joining P and Q in the ratio 2:1, (i) internally, and (ii) externally.
Solution
(i) The position vector of the point R dividing the join of P and Q internally in the ratio 2:1 is
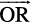 =
= 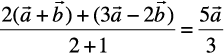
(ii) The position vector of the point R dividing the join of P and Q externally in the ratio 2:1 is
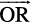 =
= 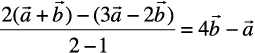
Example 12 Show that the points 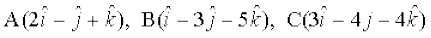 are the vertices of a right angled triangle.
are the vertices of a right angled triangle.
Solution We have
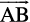 =
= 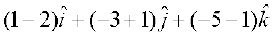
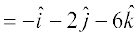
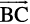 =
= 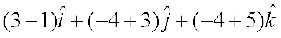
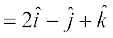
and 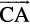 =
= 
Further, note that
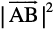 =
= 
Hence, the triangle is a right angled triangle.
Exercise 10.2
1. Compute the magnitude of the following vectors:
 =
= 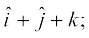
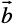 =
=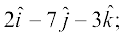
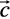 =
=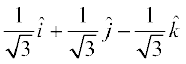
2. Write two different vectors having same magnitude.
3. Write two different vectors having same direction.
4. Find the values of x and y so that the vectors 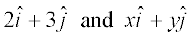 are equal.
are equal.
5. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
6. Find the sum of the vectors  =
= 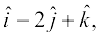
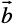 =
=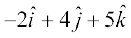 and
and 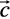 =
= .
.
7. Find the unit vector in the direction of the vector  =
=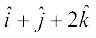 .
.
8. Find the unit vector in the direction of vector 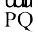 , where P and Q are the points
, where P and Q are the points
(1, 2, 3) and (4, 5, 6), respectively.
9. For given vectors,  =
= 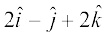 and
and 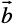 =
=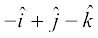 , find the unit vector in the direction of the vector
, find the unit vector in the direction of the vector 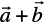 .
.
10. Find a vector in the direction of vector 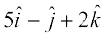 which has magnitude 8 units.
which has magnitude 8 units.
11. Show that the vectors 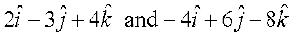 are collinear.
are collinear.
12. Find the direction cosines of the vector 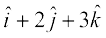 .
.
13. Find the direction cosines of the vector joining the points A(1, 2, –3) and B(–1, –2, 1), directed from A to B.
14. Show that the vector 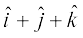 is equally inclined to the axes OX, OY and OZ.
is equally inclined to the axes OX, OY and OZ.
15. Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are 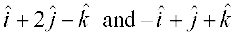 respectively, in the ratio 2 : 1
respectively, in the ratio 2 : 1
(i) internally
(ii) externally
16. Find the position vector of the mid point of the vector joining the points P(2, 3, 4) and Q(4, 1, –2).
17. Show that the points A, B and C with position vectors,  =
=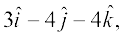
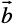 =
=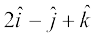 and
and 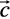 =
=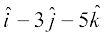 , respectively form the vertices of a right angled triangle.
, respectively form the vertices of a right angled triangle.
18. In triangle ABC (Fig 10.18), which of the following is not true:
(A) 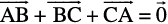
(B) 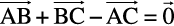
(C) 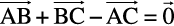
(D) 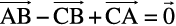

Fig 10.18
19. If 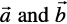 are two collinear vectors, then which of the following are incorrect:
are two collinear vectors, then which of the following are incorrect:
(A) 
(B) 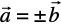
(C) the respective components of 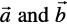 are not proportional
are not proportional
(D) both the vectors 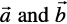 have same direction, but different magnitudes.
have same direction, but different magnitudes.
10.6 Product of Two Vectors
So far we have studied about addition and subtraction of vectors. An other algebraic operation which we intend to discuss regarding vectors is their product. We may recall that product of two numbers is a number, product of two matrices is again a matrix. But in case of functions, we may multiply them in two ways, namely, multiplication of two functions pointwise and composition of two functions. Similarly, multiplication of two vectors is also defined in two ways, namely, scalar (or dot) product where the result is a scalar, and vector (or cross) product where the result is a vector. Based upon these two types of products for vectors, they have found various applications in geometry, mechanics and engineering. In this section, we will discuss these two types of products.
10.6.1 Scalar (or dot) product of two vectors
Definition 2 The scalar product of two nonzero vectors 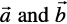 , denoted by
, denoted by  , is
, is
defined as  =
= 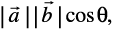
where, θ is the angle between  (Fig 10.19).
(Fig 10.19).
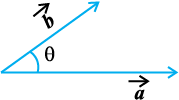
Fig 10.19
If either 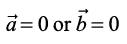 then θ is not defined, and in this case, we define
then θ is not defined, and in this case, we define 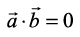
Observations
1.  is a real number.
is a real number.
2. Let 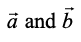 be two nonzero vectors, then
be two nonzero vectors, then 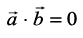 if and only if
if and only if 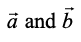 are perpendicular to each other. i.e.
are perpendicular to each other. i.e.
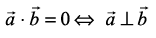
3. If θ = 0, then 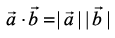
In particular, 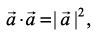 as θ in this case is 0.
as θ in this case is 0.
4. If θ = π, then 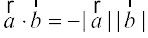
In particular, 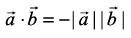 , as θ in this case is π.
, as θ in this case is π.
5. In view of the Observations 2 and 3, for mutually perpendicular unit vectors 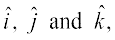 we have
we have
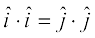 =
= 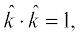
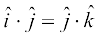 =
= 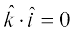
6. The angle between two nonzero vectors 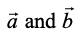 is given by
is given by
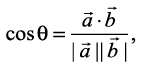 or
or 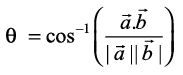
7. The scalar product is commutative. i.e.
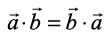 (Why?)
(Why?)
Two important properties of scalar product
Property 1 (Distributivity of scalar product over addition) Let  be any three vectors, then
be any three vectors, then
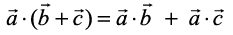
Property 2 Let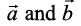 be any two vectors, and l be any scalar. Then
be any two vectors, and l be any scalar. Then
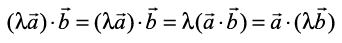
If two vectors 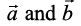 are given in component form as
are given in component form as 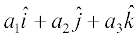 and
and 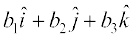 , then their scalar product is given as
, then their scalar product is given as

Thus  =
= 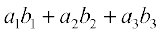
10.6.2 Projection of a vector on a line
Suppose a vector 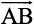 makes an angle θ with a given directed line l (say), in the anticlockwise direction (Fig 10.20). Then the projection of
makes an angle θ with a given directed line l (say), in the anticlockwise direction (Fig 10.20). Then the projection of 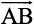 on l is a vector
on l is a vector 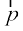 (say) with magnitude
(say) with magnitude 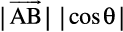 , and the direction of
, and the direction of  being the same (or opposite) to that of the line l, depending upon whether cosθ is positive or negative. The vector
being the same (or opposite) to that of the line l, depending upon whether cosθ is positive or negative. The vector  is called the projection vector, and its magnitude |
is called the projection vector, and its magnitude | | is simply called as the projection of the vector
| is simply called as the projection of the vector 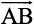 on the directed line l.
on the directed line l.
For example, in each of the following figures (Fig 10.20(i) to (iv)), projection vector of 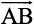 along the line l is vector
along the line l is vector  .
.
Fig 10.20
Observations
1. If 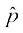 is the unit vector along a line l, then the projection of a vector
is the unit vector along a line l, then the projection of a vector  on the line l is given by
on the line l is given by 
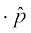 .
.
2. Projection of a vector  on other vector
on other vector 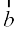 , is given by
, is given by

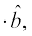 or
or 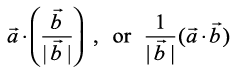
3. If θ = 0, then the projection vector of 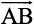 will be
will be 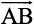 itself and if θ = π, then the projection vector of
itself and if θ = π, then the projection vector of 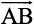 will be
will be  .
.
4. If 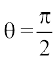 or
or 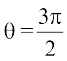 , then the projection vector of
, then the projection vector of 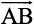 will be zero vector.
will be zero vector.
Remark If α, β and γ are the direction angles of vector 
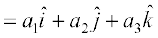 , then its direction cosines may be given as
, then its direction cosines may be given as
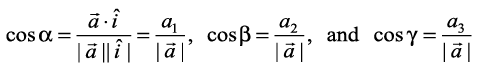
Also, note that  are respectively the projections of
are respectively the projections of  along OX, OY and OZ. i.e., the scalar components a1, a2 and a3 of the vector
along OX, OY and OZ. i.e., the scalar components a1, a2 and a3 of the vector  , are precisely the projections of
, are precisely the projections of  along x-axis, y-axis and z-axis, respectively. Further, if
along x-axis, y-axis and z-axis, respectively. Further, if  is a unit vector, then it may be expressed in terms of its direction cosines as
is a unit vector, then it may be expressed in terms of its direction cosines as


Example 13 Find the angle between two vectors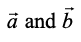 with magnitudes 1 and 2 respectively and when
with magnitudes 1 and 2 respectively and when  =1.
=1.
Solution Given 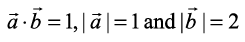 . We have
. We have
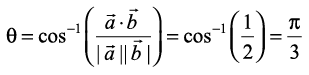
Example 14 Find angle ‘θ’ between the vectors 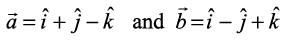 .
.
Solution The angle θ between two vectors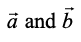 is given by
is given by
cosθ = 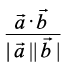
Now  =
= 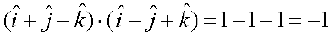 .
.
Therefore, we have cosθ = 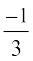
hence the required angle is θ = 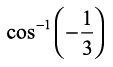
Example 15 If 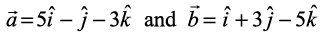 , then show that the vectors
, then show that the vectors  are perpendicular.
are perpendicular.
Solution We know that two nonzero vectors are perpendicular if their scalar product is zero.
Here 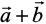 =
= 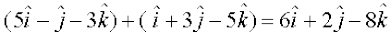
and  =
= 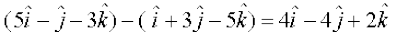
So (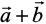 ) . (
) . ( )
) 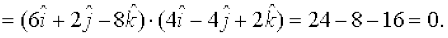
Hence 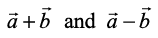 are perpendicular vectors.
are perpendicular vectors.
Example 16 Find the projection of the vector 
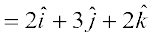 on the vector
on the vector 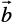
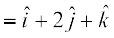 .
.
Solution The projection of vector 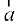 on the vector
on the vector 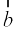 is given by
is given by
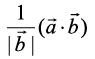 =
= 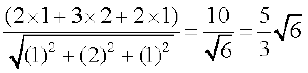
Example 17 Find  , if two vectors
, if two vectors 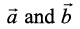 are such that
are such that 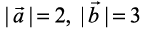 and
and 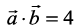 .
.
Solution We have
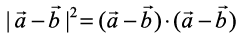
= 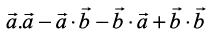
= 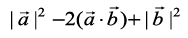
= 
Therefore  =
= 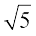
Example 18 If  is a unit vector and
is a unit vector and 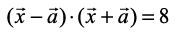 , then find
, then find 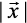 .
.
Solution Since  is a unit vector,
is a unit vector, 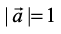 . Also,
. Also,
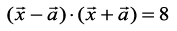
or 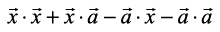 = 8
= 8
or 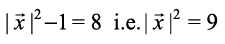
Therefore 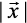 = 3 (as magnitude of a vector is non negative).
= 3 (as magnitude of a vector is non negative).
Example 19 For any two vectors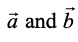 , we always have
, we always have  (Cauchy-Schwartz inequality).
(Cauchy-Schwartz inequality).
Solution The inequality holds trivially when either 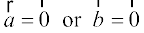 . Actually, in such a situation we have
. Actually, in such a situation we have 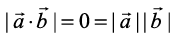 . So, let us assume that
. So, let us assume that 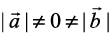 .
.
Then, we have
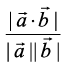 =
= 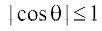
Therefore 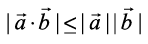
Example 20 For any two vectors , we always have
, we always have 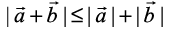 (triangle inequality).
(triangle inequality).
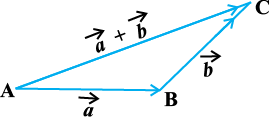
Fig 10.21
Solution The inequality holds trivially in case either 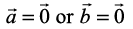 (How?). So, let
(How?). So, let 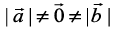 . Then,
. Then,
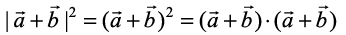
= 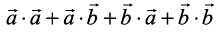
= 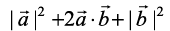 (scalar product is commutative)
(scalar product is commutative)
≤ 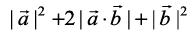 (since
(since 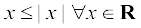 )
)
≤ 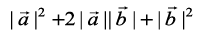 (from Example 19)
(from Example 19)
= 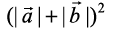
Hence 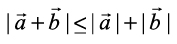
Remark If the equality holds in triangle inequality (in the above Example 20), i.e.
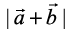 =
= 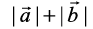 ,
,
then 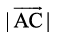 =
= 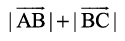
showing that the points A, B and C are collinear.
Example 21 Show that the points 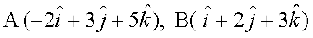 and
and 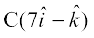 are collinear.
are collinear.
Solution We have
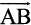 =
= 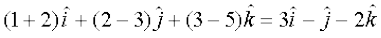 ,
,
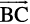 =
= 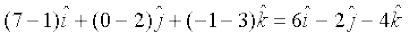 ,
,
 =
= 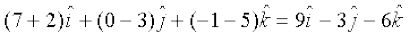
 =
= 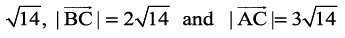
Therefore 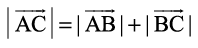
Hence the points A, B and C are collinear.
☘ Note In Example 21, one may note that although 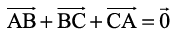 but the points A, B and C do not form the vertices of a triangle.
but the points A, B and C do not form the vertices of a triangle.
Exercise 10.3
1. Find the angle between two vectors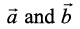 with magnitudes
with magnitudes 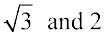 , respectively having
, respectively having  .
.
2. Find the angle between the vectors 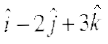 and
and 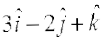
3. Find the projection of the vector 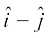 on the vector
on the vector 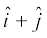 .
.
4. Find the projection of the vector 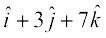 on the vector
on the vector 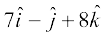 .
.
5. Show that each of the given three vectors is a unit vector:
Also, show that they are mutually perpendicular to each other.
6. Find 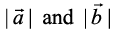 , if
, if 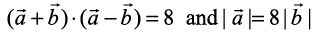 .
.
7. Evaluate the product 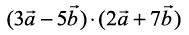 .
.
8. Find the magnitude of two vectors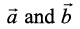 , having the same magnitude and such that the angle between them is 60o and their scalar product is
, having the same magnitude and such that the angle between them is 60o and their scalar product is  .
.
9. Find 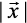 , if for a unit vector
, if for a unit vector  ,
, 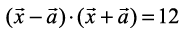 .
.
10. If 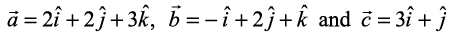 are such that
are such that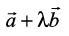 is perpendicular to
is perpendicular to 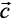 , then find the value of λ.
, then find the value of λ.
11. Show that  is perpendicular to
is perpendicular to 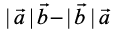 , for any two nonzero vectors
, for any two nonzero vectors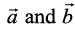 .
.
12. If  , then what can be concluded about the vector
, then what can be concluded about the vector 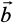 ?
?
13. If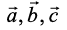 are unit vectors such that
are unit vectors such that 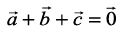 , find the value of
, find the value of  .
.
14. If either vector  . But the converse need not be true. Justify your answer with an example.
. But the converse need not be true. Justify your answer with an example.
15. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors 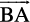 and
and 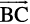 ].
].
16. Show that the points A(1, 2, 7), B(2, 6, 3) and C(3, 10, –1) are collinear.
17. Show that the vectors 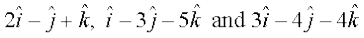 form the vertices of a right angled triangle.
form the vertices of a right angled triangle.
18. If  is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ
is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ is unit vector if
is unit vector if
(A) λ = 1 (B) λ = – 1 (C) a = |λ| (D) a = 1/|λ|
10.6.3 Vector (or cross) product of two vectors
In Section 10.2, we have discussed on the three dimensional right handed rectangular coordinate system. In this system, when the positive x-axis is rotated counterclockwise into the positive y-axis, a right handed (standard) screw would advance in the direction of the positive z-axis (Fig 10.22(i)).
In a right handed coordinate system, the thumb of the right hand points in the direction of the positive z-axis when the fingers are curled in the direction away from the positive x-axis toward the positive y-axis (Fig 10.22(ii)).

Fig 10.22 (i), (ii)
Definition 3 The vector product of two nonzero vectors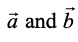 , is denoted by
, is denoted by 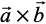 and defined as
and defined as
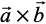 =
= 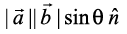 ,
,
where, θ is the angle between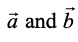 ,
, 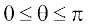 and
and 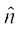 is a unit vector perpendicular to both
is a unit vector perpendicular to both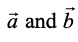 , such that
, such that 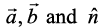 form a right handed system (Fig 10.23). i.e., the right handed system rotated from
form a right handed system (Fig 10.23). i.e., the right handed system rotated from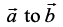 moves in the direction of
moves in the direction of 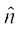 .
.
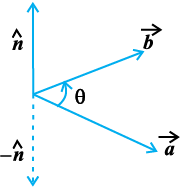
Fig 10.23
If either 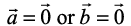 , then θ is not defined and in this case, we define
, then θ is not defined and in this case, we define 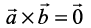 .
.
Observations
1. 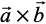 is a vector.
is a vector.
2. Let  be two nonzero vectors. Then
be two nonzero vectors. Then 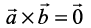 if and only if
if and only if 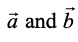 are parallel (or collinear) to each other, i.e.,
are parallel (or collinear) to each other, i.e.,
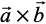 =
= 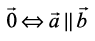
In particular, and
and , since in the first situation, θ = 0 and in the second one, θ = π, making the value of sinθ to be 0.
, since in the first situation, θ = 0 and in the second one, θ = π, making the value of sinθ to be 0.
3. If 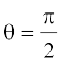 then
then 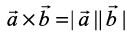 .
.
4. In view of the Observations 2 and 3, for mutually perpendicular unit vectors 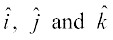 (Fig 10.24), we have
(Fig 10.24), we have
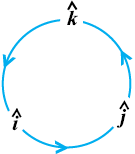
Fig 10.24
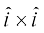 =
= 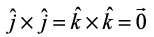
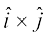 =
= 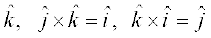
5. In terms of vector product, the angle between two vectors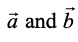 may be
may be
given as
sinθ = 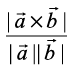
6. It is always true that the vector product is not commutative, as 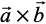 =
= 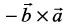 . Indeed,
. Indeed, 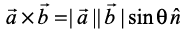 , where
, where 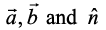 form a right handed system, i.e., θ is traversed from
form a right handed system, i.e., θ is traversed from 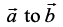 , Fig 10.25 (i). While,
, Fig 10.25 (i). While, 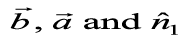 , where
, where  form a right handed system i.e. θ is traversed from
form a right handed system i.e. θ is traversed from 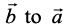 ,
,
Fig 10.25(ii).
Fig 10.25 (i), (ii)
Thus, if we assume to lie in the plane of the paper, then
to lie in the plane of the paper, then  both will be perpendicular to the plane of the paper. But,
both will be perpendicular to the plane of the paper. But, 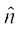 being directed above the paper while
being directed above the paper while 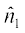 directed below the paper. i.e.
directed below the paper. i.e. 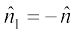 .
.
Hence 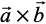 =
= 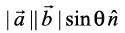
= 
7. In view of the Observations 4 and 6, we have
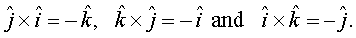
8. If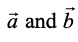 represent the adjacent sides of a triangle then its area is given as
represent the adjacent sides of a triangle then its area is given as  .
.
By of the area of a triangle, we have from Fig 10.26,
Area of triangle ABC = 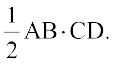
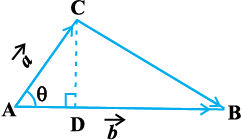
Fig 10.26
But 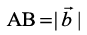 (as given), and CD =
(as given), and CD = 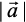 sinθ.
sinθ.
Thus, Area of triangle ABC = 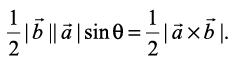
9. If 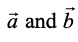 represent the adjacent sides of a parallelogram, then its area is given by
represent the adjacent sides of a parallelogram, then its area is given by 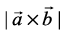 .
.
From Fig 10.27, we have
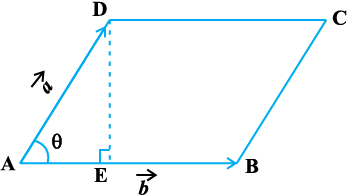
Fig 10.27
Area of parallelogram ABCD = AB. DE.
But 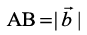 (as given), and
(as given), and
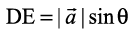 .
.
Thus,
Area of parallelogram ABCD =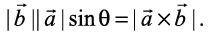
We now state two important properties of vector product.
Property 3 (Distributivity of vector product over addition): If 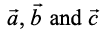 are any three vectors and λ be a scalar, then
are any three vectors and λ be a scalar, then
(i) 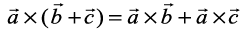
(ii) 
Let 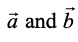 be two vectors given in component form as
be two vectors given in component form as 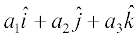 and
and 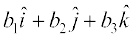 , respectively. Then their cross product may be given by
, respectively. Then their cross product may be given by
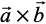 =
= 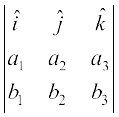

Example 22 Find 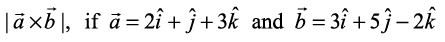
Solution We have
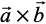 =
= 
= 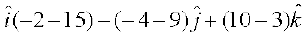
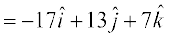
Hence 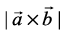 =
= 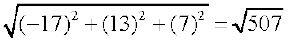
Example 23 Find a unit vector perpendicular to each of the vectors 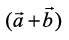 and
and 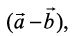 where
where 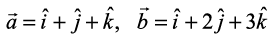 .
.
Solution We have 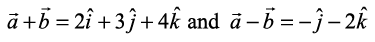
A vector which is perpendicular to both  is given by
is given by
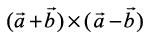 =
= 
Now 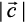 =
= 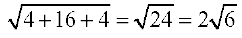
Therefore, the required unit vector is
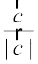 =
= 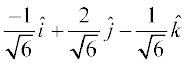
☘ Note There are two perpendicular directions to any plane. Thus, another unit vector perpendicular to  will be
will be 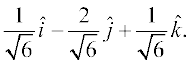 But that will be a consequence of
But that will be a consequence of  .
.
Example 24 Find the area of a triangle having the points A(1, 1, 1), B(1, 2, 3) and C(2, 3, 1) as its vertices.
Solution We have 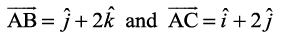 . The area of the given triangle is
. The area of the given triangle is 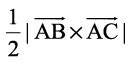 .
.
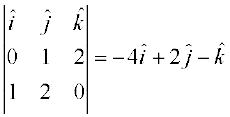
Now, 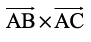 =
= 
Therefore  =
= 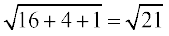
Thus, the required area is 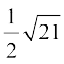
Example 25 Find the area of a parallelogram whose adjacent sides are given by the vectors 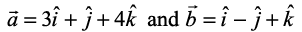
Solution The area of a parallelogram with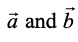 as its adjacent sides is given by
as its adjacent sides is given by 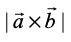 .
.
Now 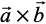 =
= 
Therefore 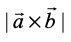 =
= 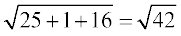
and hence, the required area is 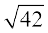 .
.
Exercise 10.4
1. Find 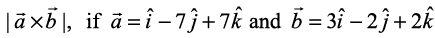 .
.
2. Find a unit vector perpendicular to each of the vector  , where
, where 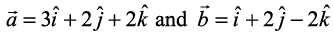 .
.
3. If a unit vector  makes angles
makes angles  and an acute angle θ with
and an acute angle θ with 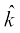 , then find θ and hence, the components of
, then find θ and hence, the components of  .
.
4. Show that
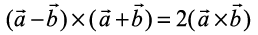
5. Find λ and µ if 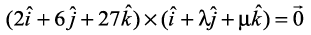 .
.
6. Given that 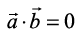 and
and 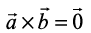 . What can you conclude about the vectors
. What can you conclude about the vectors 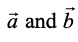 ?
?
7. Let the vectors 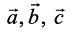 be given as
be given as 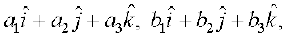
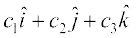 . Then show that
. Then show that 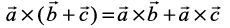 .
.
8. If either 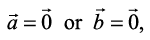 then
then 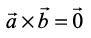 . Is the converse true? Justify your answer with an example.
. Is the converse true? Justify your answer with an example.
9. Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
10. Find the area of the parallelogram whose adjacent sides are determined by the vectors 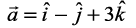 and
and 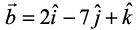 .
.
11. Let the vectors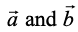 be such that
be such that 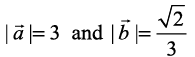 , then
, then 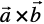 is a unit vector, if the angle between
is a unit vector, if the angle between is
is
(A) π/6 (B) π/4 (C) π/3 (D) π/2
12. Area of a rectangle having vertices A, B, C and D with position vectors 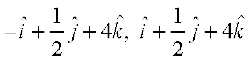 ,
, 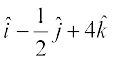 and
and 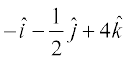 , respectively is
, respectively is
(A)  (B) 1
(B) 1
(C) 2 (D) 4
Miscellaneous Examples
Example 26 Write all the unit vectors in XY-plane.
Solution Let 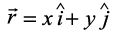 be a unit vector in XY-plane (Fig 10.28). Then, from the figure, we have x = cos θ and y = sin θ (since |
be a unit vector in XY-plane (Fig 10.28). Then, from the figure, we have x = cos θ and y = sin θ (since |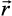 | = 1). So, we may write the vector
| = 1). So, we may write the vector 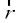 as
as
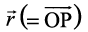 =
= 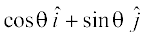 ... (1)
... (1)
Clearly, |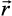 | =
| = 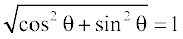

Fig 10.28
Also, as θ varies from 0 to 2π, the point P (Fig 10.28) traces the circle x2 + y2 = 1 counterclockwise, and this covers all possible directions. So, (1) gives every unit vector in the XY-plane.
Example 27 If  are the position vectors of points A, B, C and D respectively, then find the angle between
are the position vectors of points A, B, C and D respectively, then find the angle between 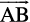 and
and 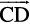 . Deduce that
. Deduce that 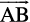 and
and 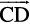 are collinear.
are collinear.
Solution Note that if θ is the angle between AB and CD, then θ is also the angle between 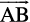 and
and 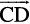 .
.
Now 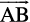 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
Since 0 ≤ θ ≤ π, it follows that θ = π. This shows that 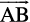 and
and 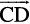 are collinear.
are collinear.
Alternatively, 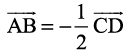 which implies that
which implies that 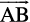 and
and  are collinear vectors.
are collinear vectors.
Example 28 Let  be three vectors such that
be three vectors such that 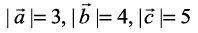 and each one of them being perpendicular to the sum of the other two, find
and each one of them being perpendicular to the sum of the other two, find 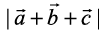 .
.
Solution Given 
Now 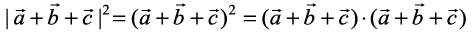
= 
+ 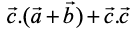
= 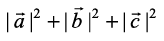
= 9 + 16 + 25 = 50
Therefore 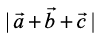 =
= 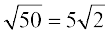
Example 29 Three vectors  satisfy the condition
satisfy the condition 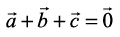 . Evaluate the quantity
. Evaluate the quantity 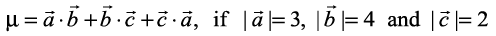 .
.
Solution Since 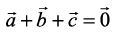 , we have
, we have
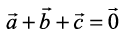 = 0
= 0
or 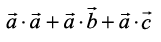 = 0
= 0
Therefore 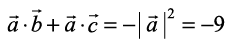 ... (1)
... (1)
Again, 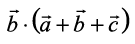 = 0
= 0
or 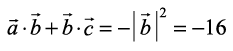 ... (2)
... (2)
Similarly 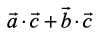 = – 4. ... (3)
= – 4. ... (3)
Adding (1), (2) and (3), we have
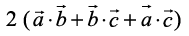 = – 29
= – 29
or 2µ = – 29, i.e., µ = 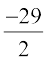
Example 30 If with reference to the right handed system of mutually perpendicular unit vectors 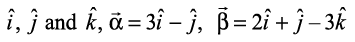 , then express
, then express 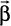 in the form
in the form 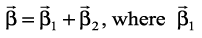 is parallel to
is parallel to 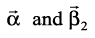 is perpendicular to
is perpendicular to 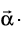
Solution Let 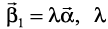 is a scalar, i.e.,
is a scalar, i.e., 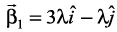 .
.
Now 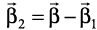 =
= 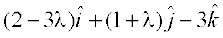 .
.
Now, since 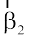 is to be perpendicular to
is to be perpendicular to 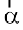 , we should have
, we should have 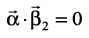 . i.e.,
. i.e.,
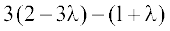 = 0
= 0
or λ = 
Therefore 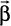 1 =
1 = 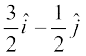 and
and 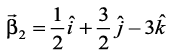
Miscellaneous Exercise on Chapter 10
1. Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
2. Find the scalar components and magnitude of the vector joining the points
P(x1, y1, z1) and Q(x2, y2, z2).
3. A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
4. If 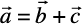 , then is it true that
, then is it true that 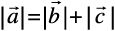 ? Justify your answer.
? Justify your answer.
5. Find the value of x for which 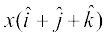 is a unit vector.
is a unit vector.
6. Find a vector of magnitude 5 units, and parallel to the resultant of the vectors 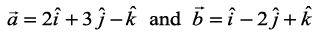 .
.
7. If 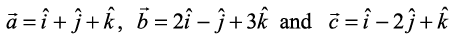 , find a unit vector parallel to the vector
, find a unit vector parallel to the vector 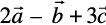 .
.
8. Show that the points A(1, – 2, – 8), B(5, 0, –2) and C(11, 3, 7) are collinear, and find the ratio in which B divides AC.
9. Find the position vector of a point R which divides the line joining two points
P and Q whose position vectors are 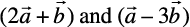 externally in the ratio
externally in the ratio
1 : 2. Also, show that P is the mid point of the line segment RQ.
10. The two adjacent sides of a parallelogram are 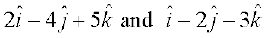 . Find the unit vector parallel to its diagonal. Also, find its area.
. Find the unit vector parallel to its diagonal. Also, find its area.
11. Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are  .
.
12. Let 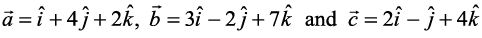 . Find a vector
. Find a vector 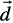 which is perpendicular to both
which is perpendicular to both  and
and 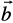 , and
, and 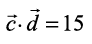 .
.
13. The scalar product of the vector 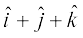 with a unit vector along the sum of vectors
with a unit vector along the sum of vectors 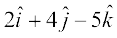 and
and 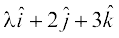 is equal to one. Find the value of λ.
is equal to one. Find the value of λ.
14. If 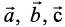 are mutually perpendicular vectors of equal magnitudes, show that the vector
are mutually perpendicular vectors of equal magnitudes, show that the vector 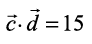 is equally inclined to
is equally inclined to  .
.
15. Prove that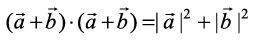 , if and only if
, if and only if 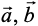 are perpendicular, given
are perpendicular, given 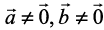 .
.
Choose the correct answer in Exercises 16 to 19.
16. If θ is the angle between two vectors 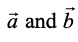 , then
, then  only when
only when
(A) 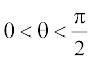 (B)
(B) 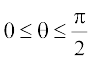
(C) 0 < θ < π (D) 0 ≤ θ ≤ π
17. Let 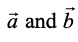 be two unit vectors and θ is the angle between them. Then
be two unit vectors and θ is the angle between them. Then 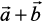 is a unit vector if
is a unit vector if
(A) 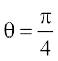 (B)
(B) 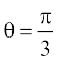 (C)
(C) 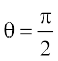 (D)
(D) 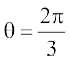
18. The value of 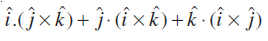
(A) 0 (B) –1 (C) 1 (D) 3
19. If θ is the angle between any two vectors 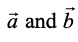 , then
, then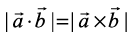 when θ is equal to
when θ is equal to
(A) 0 (B) 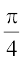 (C)
(C) 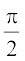 (D) π
(D) π
Summary
♦ Position vector of a point P(x, y, z) is given as 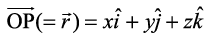 , and its magnitude by
, and its magnitude by  .
.
♦ The scalar components of a vector are its direction ratios, and represent its projections along the respective axes.
♦ The magnitude (r), direction ratios (a, b, c) and direction cosines (l, m, n) of any vector are related as:
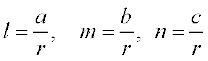
♦ The vector sum of the three sides of a triangle taken in order is 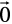 .
.
♦ The vector sum of two coinitial vectors is given by the diagonal of the parallelogram whose adjacent sides are the given vectors.
♦ The multiplication of a given vector by a scalar λ, changes the magnitude of the vector by the multiple|λ|, and keeps the direction same (or makes it opposite) according as the value of λ is positive (or negative).
♦ For a given vector  , the vector
, the vector 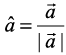 gives the unit vector in the direction of
gives the unit vector in the direction of  .
.
♦ The position vector of a point R dividing a line segment joining the points
P and Q whose position vectors are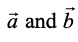 respectively, in the ratio m : n
respectively, in the ratio m : n
(i) internally, is given by 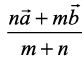 .
.
(ii) externally, is given by 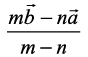 .
.
♦ The scalar product of two given vectors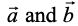 having angle θ between them is defined as
having angle θ between them is defined as
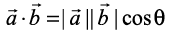 .
.
Also, when 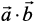 is given, the angle ‘θ’ between the vectors
is given, the angle ‘θ’ between the vectors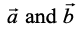 may be determined by
may be determined by
cosθ = 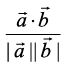
♦ If θ is the angle between two vectors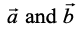 , then their cross product is given as
, then their cross product is given as

where 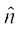 is a unit vector perpendicular to the plane containing
is a unit vector perpendicular to the plane containing 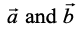 . Such that
. Such that form right handed system of coordinate axes.
form right handed system of coordinate axes.
♦ If we have two vectors 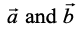 , given in component form as
, given in component form as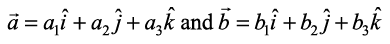 and λ any scalar,
and λ any scalar,
Historical Note
The word vector has been derived from a Latin word vectus, which means “to carry”. The germinal ideas of modern vector theory date from around 1800 when Caspar Wessel (1745-1818) and Jean Robert Argand (1768-1822) described that how a complex number a + ib could be given a geometric interpretation with the help of a directed line segment in a coordinate plane. William Rowen Hamilton (1805-1865) an Irish mathematician was the first to use the term vector for a directed line segment in his book Lectures on Quaternions (1853). Hamilton’s method of quaternions (an ordered set of four real numbers given as: 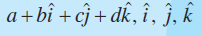
In the 1880, Josaih Willard Gibbs (1839-1903), an American physicist and mathematician, and Oliver Heaviside (1850-1925), an English engineer, created what we now know as vector analysis, essentially by separating the real (scalar) part of quaternion from its imaginary (vector) part. In 1881 and 1884, Gibbs printed a treatise entitled Element of Vector Analysis. This book gave a systematic and concise account of vectors. However, much of the credit for demonstrating the applications of vectors is due to the D. Heaviside and P.G. Tait (1831-1901) who contributed significantly to this subject.