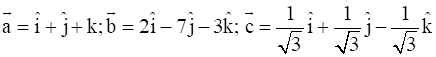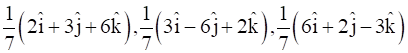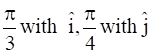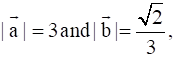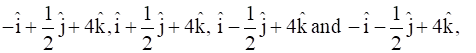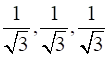Solution of Chapter 10. Vector Algebra (Mathematics Part-II Book)
Chapter Exercises
Exercise 10.1
Exercise 10.2
Exercise 10.3
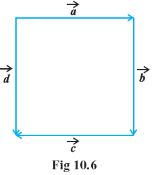
6
Find ![]() if
if ![]()