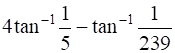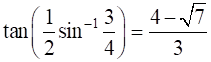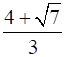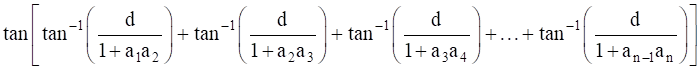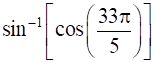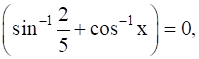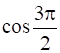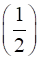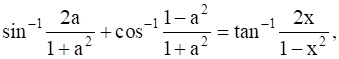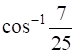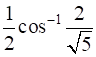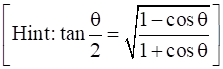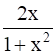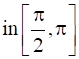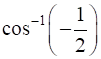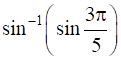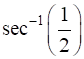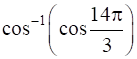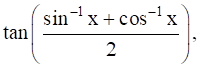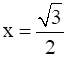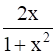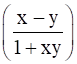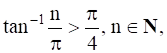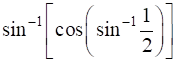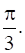Solution of Chapter 2. Inverse Trigonometric Functions (Mathematics - Exemplar Book)
Exercise
10
Show that 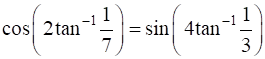 .
.
12
Prove that 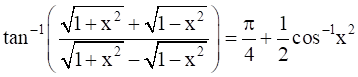
14
Prove that 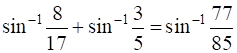 .
.
15
Show that 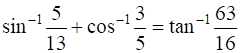
16
Prove that 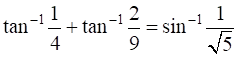 .
.
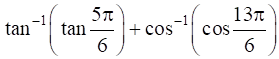
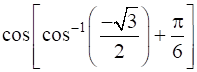
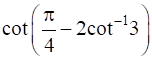
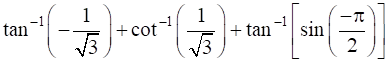
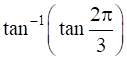
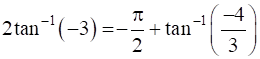
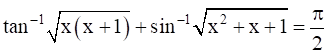
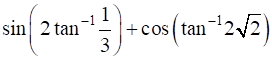
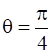
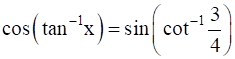
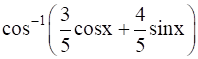
![in[ - 3 pi /4 , pi /4 ]](https://static.insightsonindia.in/ncertusercontent/solutions/?domain=gF&l=PROJ28887/1554363434711417.png)