Solution of Chapter 9. Areas of Parallelograms and Triangles (NCERT - Mathematics Book)

Which of the following figures lie on the same base and between the same parallel. In such a case, write the common base and the two parallels.

In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that

ar (EFGH) =ar (ABCD)

P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC)

In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that

(i) ar (APB) + ar (PCD) = ar(ABCD)

(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)

[Hint: Through P, draw a line parallel to AB]

In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that:

(i) ar (PQRS) = ar (ABRS)

(ii) ar (AX S) =ar (PQRS)

A farmer was having a field in the form of a parallelogram PQRS. She took any point Aon RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

In Fig.9.23, E is any point on median AD of ar Δ ABC. Show that ar (ABE) = ar (ACE).

In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) =1/4 ar(ABC)

Show that the diagonals of a parallelogram divide it into four triangles of equal area

In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).

D, E and F are respectively the mid-points of the sides BC, CA and AB of a Δ ABC. Show that:

(i) BDEF is a parallelogram.

(ii) ar (DEF) =ar (ABC)

(iii) ar (BDEF) =ar (ABC)

In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.

If AB = CD, then show that:

(i) ar (DOC) = ar (AOB)

(ii) ar (DCB) = ar (ACB)

(iii) DA || CB or ABCD is a parallelogram.

[Hint: From D and B, draw perpendiculars to AC]

D and E are points on sides AB and AC respectively of Δ ABC such that ar (DBC) = ar (EBC). Prove that DE || BC

XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)

The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see Fig. 9.26). Show that ar (ABCD) = ar (PBQR).

[Hint: Join AC and PQ. Now compare ar (ACQ) and ar (APQ)]

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC)

In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:

(i) ar (ACB) = ar (ACF)

(ii) ar (AEDF) = ar (ABCDE)

A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot soas to form a triangular plot. Explain how this proposal will be implemented.

ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY)

[Hint: Join CX]

In Fig.9.28, AP || BQ || CR. Prove that:

ar (AQC) = ar (PBR)

Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.

In Fig.9.29, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

In Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC)

Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?

[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into unequal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas]

In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ)

[Hint: Join AC]

In Fig.9.33, ABC and BDE are two equilateraltriangles such that D is the mid-point of BC. If AEintersects BC at F, show that

(i) ar (BDE) =ar (ABC)

(ii) ar (BDE) =ar (BAE)

(iii) ar (ABC) = 2 ar (BEC)

(iv) ar (BFE) = ar (AFD)

(v) ar (BFE) = 2 ar (FED)

(vi) ar (FED) =ar (AFC)

[Hint: Join EC and AD.

Show that BE || AC and DE || AB, etc]

Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).

[Hint: From A and C, draw perpendiculars to BD]

P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that

(i) ar (PRQ) =ar (ARC)

(ii) ar (RQC) =ar (ABC)

(iii) ar (PBQ) = ar (ARC)

In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:

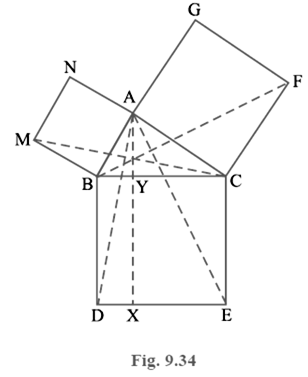
(i) Δ MBC ≅Δ ABD

(ii) ar (BYXD) = 2 ar (MBC)

(iii) ar (BYXD) = ar (ABMN)

(iv) Δ FCB ≅Δ ACE

(v) ar (CYXE) = 2 ar (FCB)

(vi) ar (CYXE) = ar (ACFG)

(vii) ar (BCED) = ar (ABMN) + ar (ACFG)

Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X