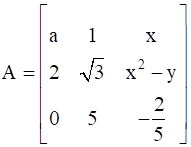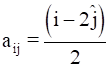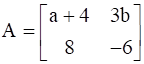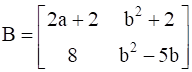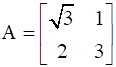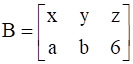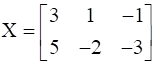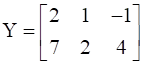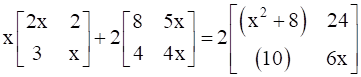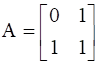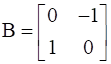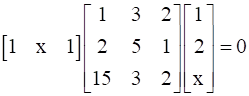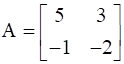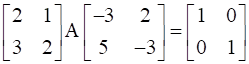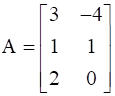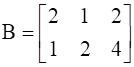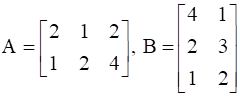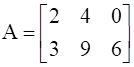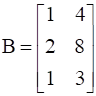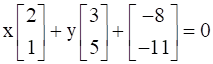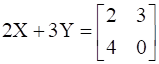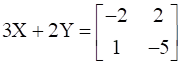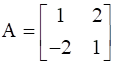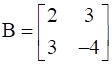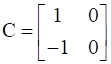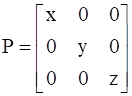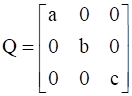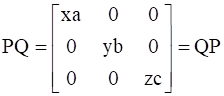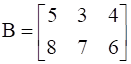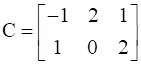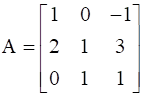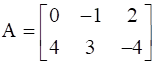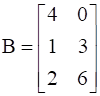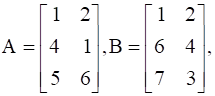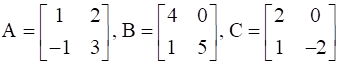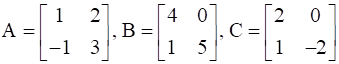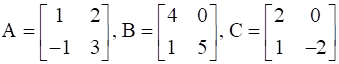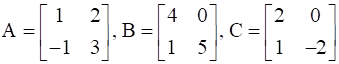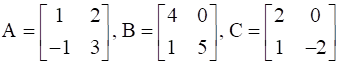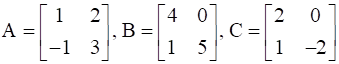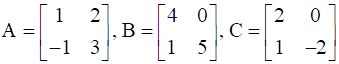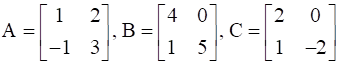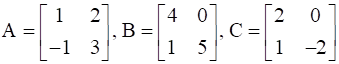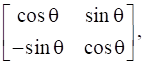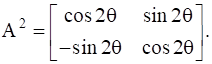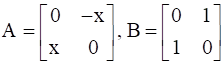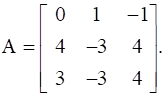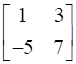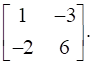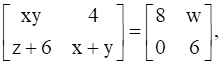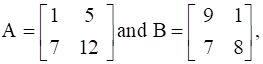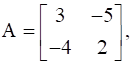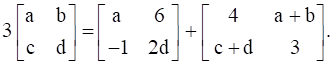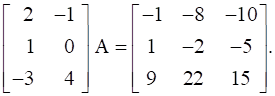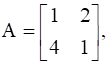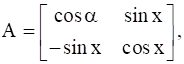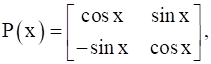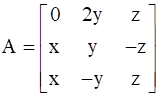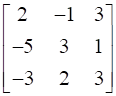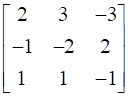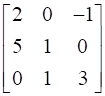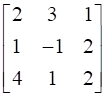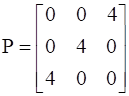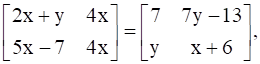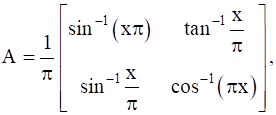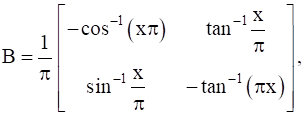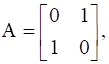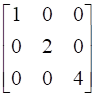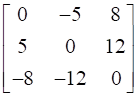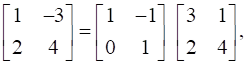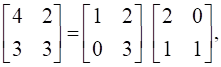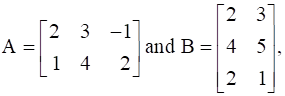Solutions of chapter 3. Matrices | Mathematics - Exemplar

1

If a matrix has 28 elements, what are the possible orders it can have? What if it has 13 elements?

2

In the matrix , write:

(i) The order of the matrix A

(ii) The number of elements

(iii) Write elements a₂₃, a₃₁, a₁₂

3

Construct a_2×2 matrix where

(i)

(ii) a_ij = |– 2i + 3j|

4

Construct a 3 × 2 matrix whose elements are given by a_ij = e^ixsin jx

5

Find values of a and b if A = B, where

and

6

If possible, find the sum of the matrices A and B, where and .

7

If and find

(i) X + Y

(ii) 2X – 3Y

(iii) A matrix Z such that X + Y + Z is a zero matrix.

8

Find non-zero values of x satisfying the matrix equation:

9

If and , show that (A + B) (A – B) ≠ A² – B².

10

Find the value of x if

11

Show that satisfies the equation A² – 3A – 7I = 0 and hence find A^–1.

12

Find the matrix A satisfying the matrix equation:

13

Find A, if .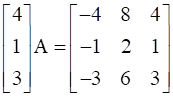

14

If and , then verify (BA)² ≠ B²A².

15

If possible, find BA and AB, where

16

Show by an example that for A ≠ O, B ≠ O, AB = O.

17

Given and . Is (AB)’ = B’A’?

18

Solve for x and y:

19

If X and Y are 2 × 2 matrices, then solve the following matrix equations for X and Y

,

20

If A = [3 5], B = [7 3], then find a non-zero matrix C such that AC = BC.

21

Given an example of matrices A, B and C such that AB = AC, where A is non-zero matrix, but B ≠ C.

22

If , and , verify:

(i) (AB) C = A (BC)

(ii) A(B + C) = AB + AC

23

If , , prove that

24

If 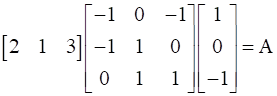, find A.

25

If , and , verify that A(B + C) = (AB + AC).

26

If , then verify that A² + A = A(A + I), where I is 3 × 3 unit matrix.

27

If and , then verify that:

(i) (A’)’ = A

(ii) (AB)’ = B’A’

(iii) (kA)’ = (kA’).

28

If then verify that:

(i) (2A + B)’ = 2A’ + B’

(ii) (A – B)’ = A’ – B’.

29

Show that A’A and AA’ are both symmetric matrices for any matrix A.

30

Let A and B be square matrices of the order 3 × 3. Is (AB)² = A²B² ? Give reasons.

31

Show that if A and B are square matrices such that AB = BA, then (A + B)² = A² + 2AB + B².

32

Let and a = 4, b = –2.

Show that:

A + (B + C) = (A + B) + C

32

Let and a = 4, b = –2.

Show that:

A(BC) = (AB)C

32

Let and a = 4, b = –2.

Show that:

(a + b)B = aB + bB

32

Let and a = 4, b = –2.

Show that:

a(C – A) = aC –aA

32

Let and a = 4, b = –2.

Show that:

(A^T)^T = A

32

Let and a = 4, b = –2.

Show that:

(bA)^T = bA^T

32

Let and a = 4, b = –2.

Show that:

(AB)^T = B^T A^T

32

Let and a = 4, b = –2.

Show that:

(A – B)C = AC – BC

32

Let and a = 4, b = –2.

Show that:

(A – B)^T = A^T – B^T

33

If then show that

34

If and x² = –1, then show that (A + B)² = A² + B².

35

Verify that A² = I when

36

Prove by Mathematical Induction that (A’)ⁿ = (Aⁿ)’, where n ∈ N for any square matrix A.

37

Find inverse, by elementary row operations (if possible), of the following matrices.

37

Find inverse, by elementary row operations (if possible), of the following matrices.

38

If then find values of x, y, z and w.

39

If find a matrix C such that 3A + 5B + 2C is a null matrix.

40

If then find A² – 5A – 14I. Hence, obtain A³.

41

Find the value of a, b, c and d, if

42

Find the matrix A such that

43

If find A² + 2A + 7I

44

If and A^–1 = A’, find value of α.

45

If the matrix is a skew symmetric matrix, find the values of a, b and c.

46

If then show that

P(x).P(y) = P(x + y) = P(y).P(x)

47

If A is square matrix such that A² = A, show that (I + A)³ = 7A + I.

48

If A, B are square matrices of same order and B is a skew-symmetric matrix, show that A’ BA is skew symmetric.

49

If AB = BA for any two square matrices, prove by mathematical induction that (AB)ⁿ = Aⁿ Bⁿ.

50

Find x, y, z if satisfies A’ = A^–1

51

If possible, using elementary row transformations, find the inverse of the following matrices

51

If possible, using elementary row transformations, find the inverse of the following matrices

51

If possible, using elementary row transformations, find the inverse of the following matrices

52

Express the matrix as the sum of a symmetric and a skew symmetric matrix.

53

The matrix is a

54

Total number of possible matrices of order 3 × 3 with each entry 2 or 0 is

55

If then the value of x + y is

56

If then A – B is equal to

57

If A and B are two matrices of the order 3 × m and 3 × n, respectively, and m = n, then the order of matrix (5A – 2B) is

58

If then A² is equal to

59

If matrix , where a_ij = 1 if i ≠ j

a_ij = 0 if i = j, then A² is equal to

60

The matrix is a

61

The matrix is a

62

If A is matrix of order m × n and B is a matrix such that AB’ and B’A are both defined, then order of matrix B is

63

If A and B are matrices of same order, then (AB’ – BA’) is a

64

If A is a square matrix such that A² = I, then (A – I)³ + (A + I)³ – 7A is equal to

65

For any two matrices A and B, we have

66

On using elementary column operations C₂→ C₂ — 2C₁ in the following matrix equation

we have:

67

On using elementary row operation R₁→ R₁ — 3R₂ in the following matrix equation:

we have:

68

Fill in the blanks in each of the

______ matrix is both symmetric and skew symmetric matrix.

68

Fill in the blanks in each of the

______ matrix is both symmetric and skew symmetric matrix.

69

Fill in the blanks in each of the

Sum of two skew symmetric matrices is always _______ matrix.

69

Fill in the blanks in each of the

Sum of two skew symmetric matrices is always _______ matrix.

70

Fill in the blanks in each of the

The negative of a matrix is obtained by multiplying it by ________.

70

Fill in the blanks in each of the

The negative of a matrix is obtained by multiplying it by ________.

71

Fill in the blanks in each of the

The product of any matrix by the scalar _____ is the null matrix.

71

Fill in the blanks in each of the

The product of any matrix by the scalar _____ is the null matrix.

72

Fill in the blanks in each of the

A matrix which is not a square matrix is called a _____ matrix.

72

Fill in the blanks in each of the

A matrix which is not a square matrix is called a _____ matrix.

73

Fill in the blanks in each of the

Matrix multiplication is _____ over addition.

73

Fill in the blanks in each of the

Matrix multiplication is _____ over addition.

74

Fill in the blanks in each of the

If A is a symmetric matrix, then A³ is a ______ matrix.

74

Fill in the blanks in each of the

If A is a symmetric matrix, then A³ is a ______ matrix.

75

Fill in the blanks in each of the

If A is a skew symmetric matrix, then A² is a _________.

75

Fill in the blanks in each of the

If A is a skew symmetric matrix, then A² is a _________.

76

Fill in the blanks in each of the

If A and B are square matrices of the same order, then

(i) (AB)’ = ________.

(ii) (kA)’ = ________. (k is any scalar)

(iii) [k (A – B)]’ = ________.

76

Fill in the blanks in each of the

If A and B are square matrices of the same order, then

(i) (AB)’ = ________.

(ii) (kA)’ = ________. (k is any scalar)

(iii) [k (A – B)]’ = ________.

77

Fill in the blanks in each of the

If A is skew symmetric, then kA is a ______. (k is any scalar)

77

Fill in the blanks in each of the

If A is skew symmetric, then kA is a ______. (k is any scalar)

78

Fill in the blanks in each of the

If A and B are symmetric matrices, then

(i) AB – BA is a _________.

(ii) BA – 2AB is a _________.

78

Fill in the blanks in each of the

If A and B are symmetric matrices, then

(i) AB – BA is a _________.

(ii) BA – 2AB is a _________.

79

Fill in the blanks in each of the

If A is symmetric matrix, then B’AB is _______.

79

Fill in the blanks in each of the

If A is symmetric matrix, then B’AB is _______.

80

Fill in the blanks in each of the

If A and B are symmetric matrices of same order, then AB is symmetric if and only if ______.

80

Fill in the blanks in each of the

If A and B are symmetric matrices of same order, then AB is symmetric if and only if ______.

81

Fill in the blanks in each of the

In applying one or more now operations while finding A^–1 by elementary row operations, we obtain all zeros in one or more, then A^–1 ______.

81

Fill in the blanks in each of the

In applying one or more now operations while finding A^–1 by elementary row operations, we obtain all zeros in one or more, then A^–1 ______.

82